计算机视觉中的Transformer续

上一篇文章《计算机视觉中的Transformer》讲了计算机视觉中的Transformer结构^[1]，还有非常受欢迎的Vision Transformer(ViT)^[2]。本篇文章将补上上一篇掠过的《Attention Augmented Convolutional Networks》^[3]和《End-to-End Object Detection with Transformers》^[4]，同时也会介绍一下DeiT (Data-effieciency Image Transformer)^[5]。

Self-Attention回顾

Transformer的核心是Self-Attention。Self-Attention是基于特征向量对序列上token成对关系的表征学习(Representation Learning)。

Fig. 1. Self Attention.

计算方式大致如下:

序列: $X\in R^{n\times d}$
Query向量: $Q$有相对应的可学习权重$W^Q\in R^{n\times dq}$
Key向量: $K$也有相对应的可学习权重$W^K\in R^{n\times dk}$
Value向量: $V$也有相对应的可学习权重$W^V\in R^{n\times dv}$
$Q=XW^Q, K=XW^K, V=XW^V$
Self-Attention层: $Z=softmax(\frac{QK^T}{\sqrt{d_q}})V$
若是Masked Self-Attention层，则需要增加一层mask: $softmax(\frac{QK^T}{\sqrt{d_q}}\circ M)$

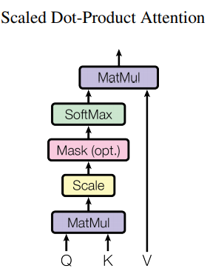
Fig. 2. Self Attention运算过程. Adapted from ^[1]

这里展示的是一个简单的Self-Attention计算方式，对于^[1]同时提出的Multi-Head Self-Attention，可以将上述过程并行的执行多次来模拟不同的head。

在2021年，计算机视觉领域中的Transformer和Self-Attentio的相关技术已经发展了很多。我们可以使用以下这张图来理解今天的Self-Attention相关技术的不同类型。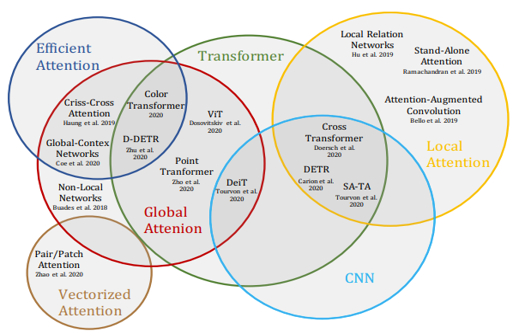

Fig. 3. Self Attention不同类型. Adapted from ^[6]

在上图中能看到不同的Attention类型，比如Local Attention, Global Attention, Vectorized Attention。下图介绍了这些类型的大致计算流程。

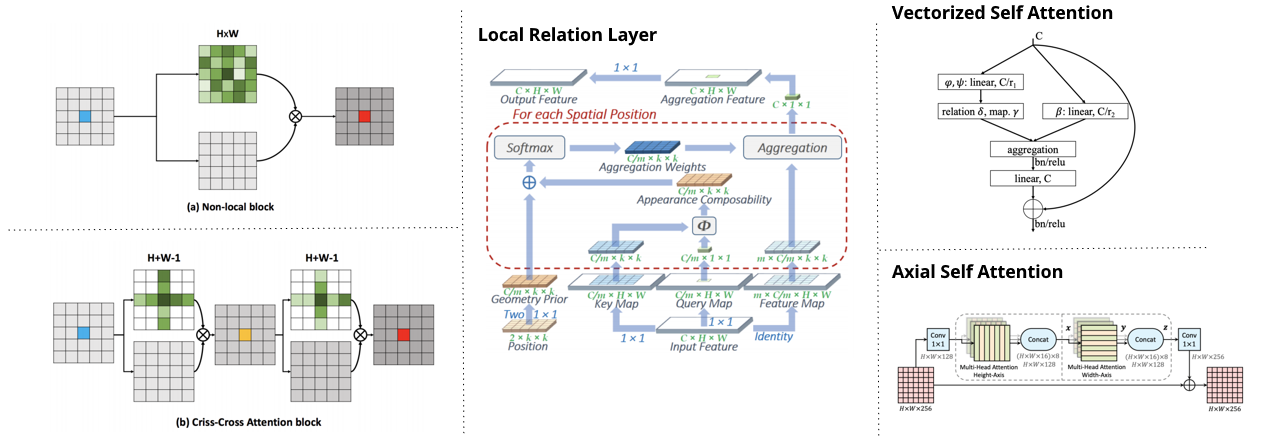
Fig. 4. Self Attention的不同类型. Adapted from ^[6]

用Attention增强卷积

从之前我们可以了解到，Self-Attention可以很好的找到距离较远的token之间的关系，而普通的卷积层只能计算非常有限的范围。如果我们能够将这些距离较远的token之间的关系计算出来，那么就可以使用Self-Attention来弥补卷积层的这个缺陷，对图像分析是有帮助的。而且卷积层是等变的，在不同区域的卷积用的是同一个参数。所以在2019年的时候，这篇文章的作者看到Self-Attention已经被广泛运用于NLP领域，所以就想到了用Self-Attention来增强卷积，并且使用基于相对位置的Positional Encoding用于解决上述说的等变问题^[3]。

Flatten和Attention层

先介绍会在这个部分中使用的一些数学符号:

$H, W, F_in$是指特征图中高度、宽度、输入feature map的数量
$N_h, d_v, d_k$是指head的数量，value和key的维度。其中$N_h$是可以整除$d_v$和$d_k$的。
$d^h_v, d^h_k$是指每一个head中value和key的维度。

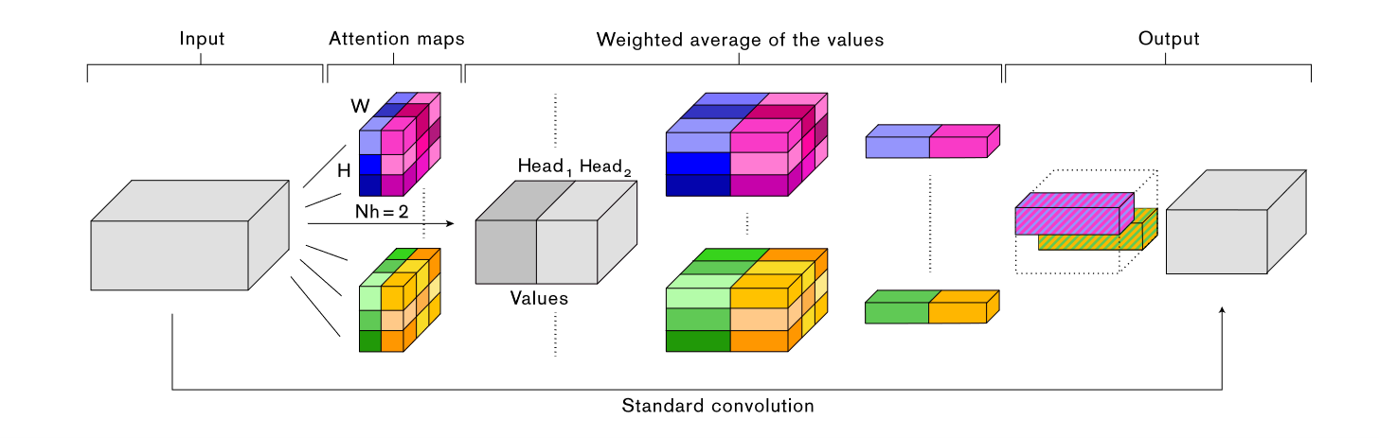
Fig. 5. Attention Augmented Convolution的计算过程. Adapted from ^[3]

第一步是需要将输入的特征图进行flatten，从$(H,W,F_in)$变成一个新矩阵$X\in \mathbb{R}^{HW\times F_{in}}$。然后把它放进标准的Multi-head Attention(MHA)层中，于是输出它的输出则是，
$$O_h=Softmax(\frac{(XW_q)(XW_k)^T}{\sqrt{d^h_k}})(XW_v)$$

Positional Encoding

在这篇文章，作者使用了一个基于像素的相对位置的Positional Encoding，专门用于图像分析。其实这个相对位置的Positional Encoding之前已经提出，具体的可以参考这篇^[7]。

它的计算方式是

$$l_{i,j}=\frac{q_i^T}{\sqrt{d_k^h}}(k_j+r^W_{j_x-i_x}+r^H_{j_y-i_y})$$

其中$r$是Positional Encoding，$i$是当前token所代表的像素，$j$是计算Self-Attention时的目标像素，而$x$和$y$则是像素的位置。将这个计算向量化后，

$$O_h=Softmax(\frac{QK^T+S_H^{rel}+S_W^{rel}}{\sqrt{d^h_k}})V$$

这篇作者也提到，根据他们的实验，最好的效果是同时使用传统卷积层和Attention层的输出，所以以上的结果要通过一个简单的拼接层来获得。

$$AAConv(X)=Concat[Conv(X),MHA(X)]$$

实验结果

首先是每篇论文都会提到的自己的方法比别人强。

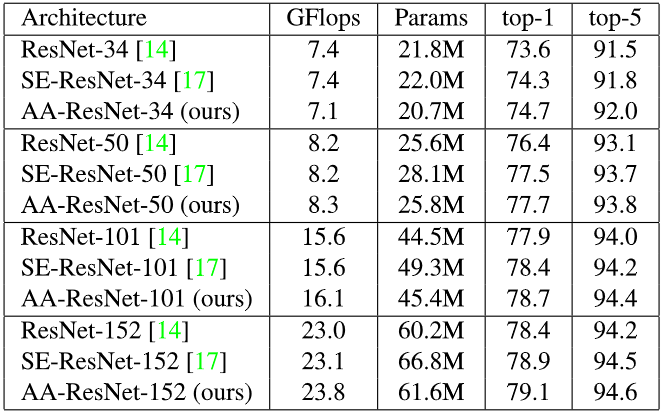
Fig. 6. Attention Augmented用于分类的实验结果. Adapted from ^[3]

可见，用于一些传统的CNN模型，用Attention增强卷积的方法可以得到更好的结果。对于COCO数据集的对象检测也是一样的，这里就不再赘述了。

不过其中最有趣的还是Positional Encoding的对比。

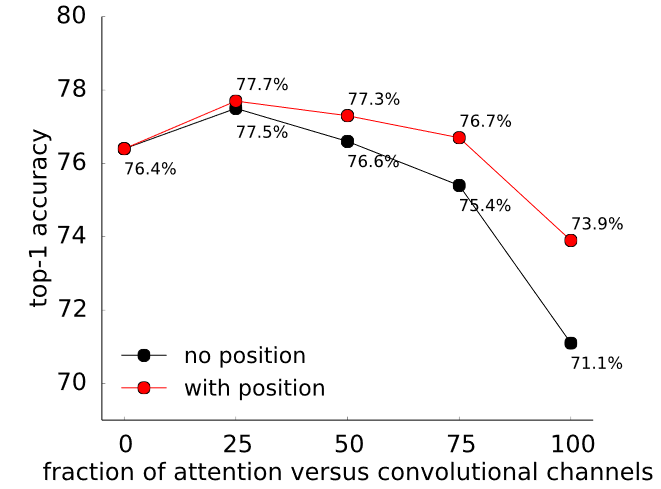
Fig. 7. Positional Encoding是否使用的对比结果. Adapted from ^[3]

能看到这个Positional Encoding真的是很有用，所以在Transformer中的Self-Attention层中基本人人都会用它。

E2E的Transformer对象检测

在2020年的时候，一篇论文^[4]提出了一个E2E的Transformer对象检测模型Detection Transformer (DETR)，它非常有开创性的使用Transformer结构实现了一个完全端到端的训练方式。这有什么好处呢？首先之前的对象检测模型很多都是需要Proposal，Anchor，或者Window之类的容易出错，而且还需要一些人工处理，比如说非最大值抑制等等。这些东西在一定程度上会影响模型的性能。如果能使用E2E的模式避免人工处理的情况下训练，那就能解决这个问题。

首先来看一下它的结构。

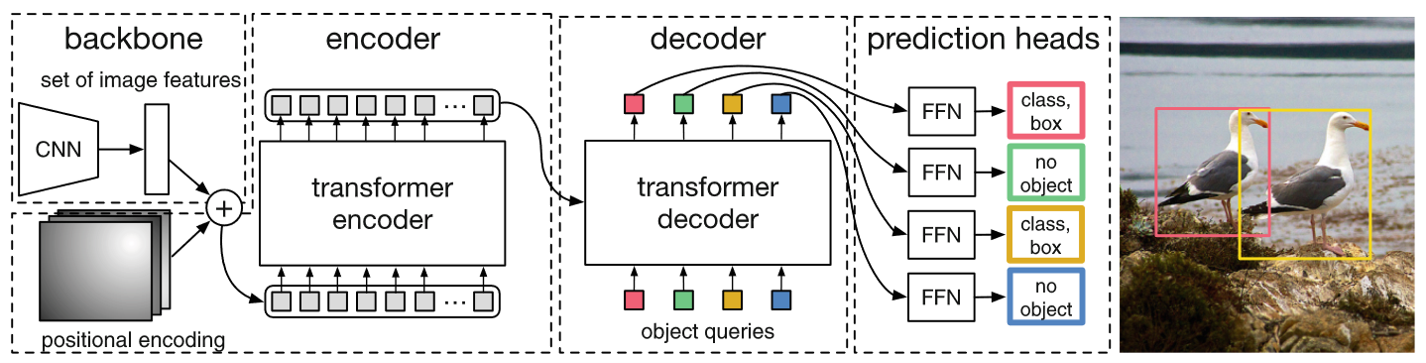
Fig. 8. DETR结构. Adapted from ^[4]

这个结构是由一个骨干网络，Positional Encoding，Transformer，以及一个FFN预测头组成的。让我们一个一个看。

骨干特征提取器

首先是第一步的backbone，这一部分在原文中是一个CNN的特征提取器，需要从图像中提取出高价值的特征图。在原文中对于一个图像为$x_{img}\in \mathbb{R}^{3\times H_0 \times W_0}$，在骨干网络后将会变成一个特征图$f\in \mathbb{R}^{C\times H\times W}$。他们设定的值是$C=2048$ $H,W=\frac{H_0}{32},\frac{W_0}{32}$ 。

Transformer部分

通过骨干网络得到的特征图会通过一个1x1卷积压缩通道数，得到$z_0\in\mathbb{R}^{d\times H\times W}$。因为这个Transformer编码器希望得到一个序列作为输入，所以不能用一个三维的矩阵，需要压平成二维。这个特征图将会被flatten到$(d\times HW)$。对于每一层Transformer编码器，都有一个Self-Attention层和FFN，就像原版Transformer一样。作者还特地说明了，对于每一层，都添加了一个固定的不可训练的Positional Encoding加到输入中去。对于Self-Attention层和Transformer编码器部分相信大家都很熟悉了，但是这个网络还使用了Transformer解码器部分，这需要好好看看。

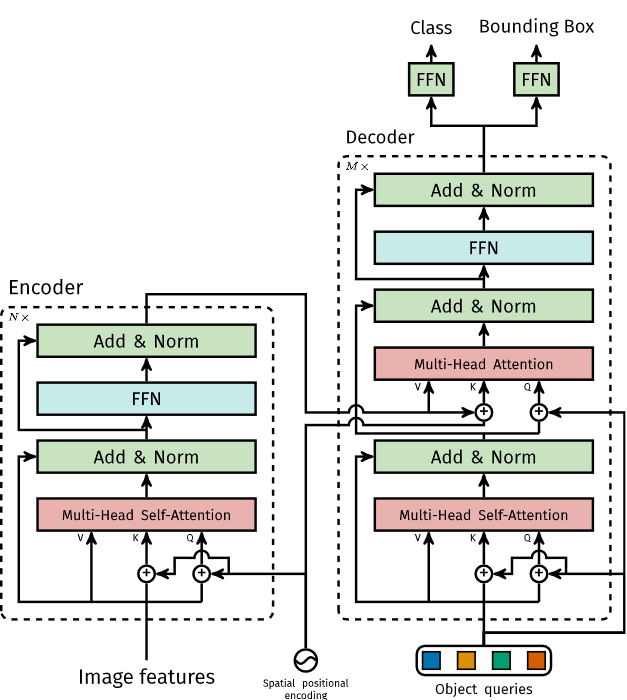
Fig. 9. DETR中的Transformer部分. Adapted from ^[4]

这里我们可以看到，它并没使用原版Transformer中的Masked Multi-Head Self-Attention层，可能是因为原版的是对于时间序列的预测所以需要遮盖未来时间的序列元素，但是这里是图像分析，则不需要这些。然后是对于编码器的Attention层，和解码器的第二个Attention层，都使用了Positional Encoding，而且是每一层都会使用。

这里的Object queries其实是一个可学习的参数，原文中设定的长度是$N=100$。剩下的都是一些相加融合，根据这张图应该是很容易理解的。

FFN预测头

在解码器的输出得到嵌入序列之后，对于序列中的每一个元素都通过两个FFN网络，一个用于预测类型，一个用于预测Box。

这些FFN在原文中使用的是一个3层MLP和ReLU。对于一个91个类的多分类问题，这里的类型预测FFN会输出一个92长度的向量，多出来的一个代表”没有对象($\phi$)”。这个预测Box会被编码成中心坐标(x, y)和宽度高度(w, h)，也就是长度为4的向量。由于这个预测框的数量等于Object Queriesd的数量$N$且是固定且有限的，所以必须要远大于实际可能的预测框数量。

损失函数

因为预测出的是长度为$N$的一系列无序的box，而ground truth是一个长度远小于$N$的序列。所以在计算损失时，需要将预测的box和ground truth进行匹配。这里需要搜索到一个有最小损失值的box匹配，然后计算这个最小损失。这个匹配$\sigma$是:

$$\hat{\sigma}=\mathop{\arg\min}_{\sigma\in\mathfrak{S}_N}\sum^N_i \mathcal{L}_{match}(y_i,\hat{y}_{\sigma(i)})$$

对于这个问题，使用Hungarian算法可以有效的解决，找到ground truth和预测结果的最优匹配。这里的$\mathcal{L}_{match}$是一个二分图匹配的损失函数，其中$y_i$是ground truth的第i个box，$\hat{y}_{\sigma(i)}$是预测的第i个box。对于第i个预测$\sigma(i)$，定义类别$c_i$的概率是$\hat{p}_{\sigma(i)}(c_i)$，预测的box是$\hat{b}_{\sigma(i)}$。定义这个损失函数为：

$$\mathcal{L}_{match}=-\mathbb{1}_{\{c_i\neq\emptyset\}}\hat{p}_{\sigma(i)}(C_i)+\mathbb{1}_{\{c_i\neq\emptyset\}}\mathcal{L}_{box}(b_i,\hat{b}_{\sigma(i)})$$

与上面的等式结合，可以得到Hungarian损失函数，

$$\mathcal{L}_{Hungarian}(y,\hat{y})=\sum^N_{i=1}[-log\hat{p}_{\hat{\sigma}(i)}(C_i)+\mathbb{1}_{\{c_i\neq\emptyset\}}\mathcal{L}_{box}(b_i,\hat{b}_{\hat{\sigma}}(i))]$$

其中的$\hat{\sigma}$是上面找到的最佳匹配方式。

对于box损失，这里使用GIOU损失函数^[8]。

再对L1损失和IOU损失进行线性组合，得到最终的损失函数，

$$\mathcal{L}=\lambda_{iou}\mathcal{L}_{iou}(b_i,\hat{b}_{\sigma(i)})+\lambda_{L1}||b_i-\hat{b}_{\sigma(i)}||_1$$

其中的$\lambda_{iou}$和$\lambda_{L1}$是超参数。

然而除此之外，他们还使用了解码器辅助损失(Auxiliary decoding loss)。添加到每一个解码器层后面，预测class和box并计算上述损失$\mathcal{L}$。

推断代码

作者们另外提供了一个基于PyTorch的用于推断的代码，放在这里有助于理解。

import torch
from torch import nn
from torchvision import resnet50

class DETR(nn.Module):

  def __init__(self, num_classes, hidden_dim, nheads, num_encoder_layers, num_decoder_layers):
    super().__init__()
    # We take only convolutional layers from ResNet-50 model
    self.backbone = nn.Sequential(*list(resnet50(pretrained=True).children())[:-2])
    self.conv = nn.Conv2d(2048, hidden_dim, 1)
    self.transformer = Transformer(hidden_dim, nheads, num_encoder_layers, num_decoder_layers)
    self.linear_class = nn.Linear(hidden_dim, num_classes + 1)
    self.linear_bbox = nn.Linear(hidden_dim, 4)
    self.query_pos = nn.Parameter(torch.randn(100, hidden_dim))
    self.row_embed = nn.Parameter(torch.randn(50, hidden_dim // 2))
    self.col_embed = nn.Parameter(torch.randn(50, hidden_dim // 2))

  def forward(self, inputs):
    x = self.backbone(inputs)
    h = self.conv(x)
    H, W = h.shape[-2:]
    pos = torch.cat([
        self.col_embed[:W].unsqueeze(0).repeat(H, 1, 1),
        self.row_embed[:H].unsqueeze(1).repeat(1, W, 1)
    ], dim=-1).flatten(0, 1).unsqueeze(1)
    h = self.transformer(pos + h.flatten(2).permute(2, 0, 1), self.query_pos.unsqueeze(1))
    return self.linear_class(h), self.linear_bbox(h).sigmoid()

detr = DETR(num_classes=91, hidden_dim=256, nheads=8, num_encoder_layers=6, 
  num_decoder_layers=6
)
detr.eval()
inputs = torch.randn(1, 3, 800, 1200)
logits, bboxes = detr(inputs)

Listing 1: DETR PyTorch推断代码. Adapted from ^[4]

实验结果

他们使用了COCO数据集用于测试这个方法。

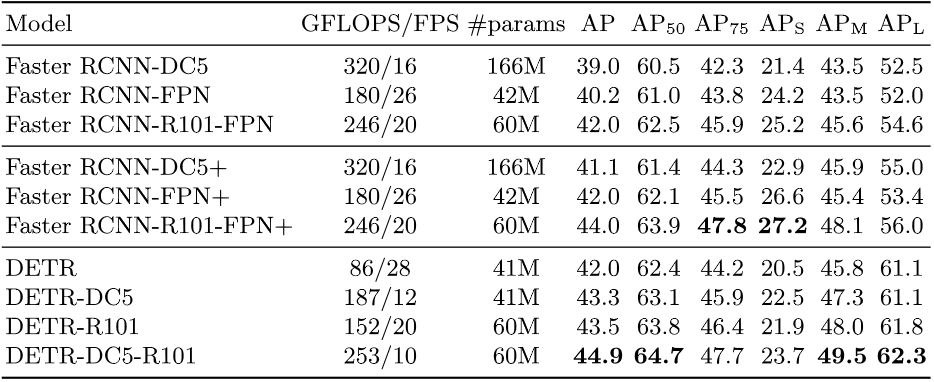
Fig. 10. DETR实验结果. Adapted from ^[4]

一言以蔽之，相比于FasterRCNN，DETR更好。

然后他们也测试了一下编码器层的数量，解码器层的数量，辅助损失，FFN，Positional Encoding的重要性，发现都很重要，都是需要的。

Fig. 11. $N$个Object Queries的预测可视化. Adapted from ^[4]

通过上图可以看出，这些预测插槽也已经学习到了box的预测模式，每一个插槽是专注于其中的少数几种box的样式。

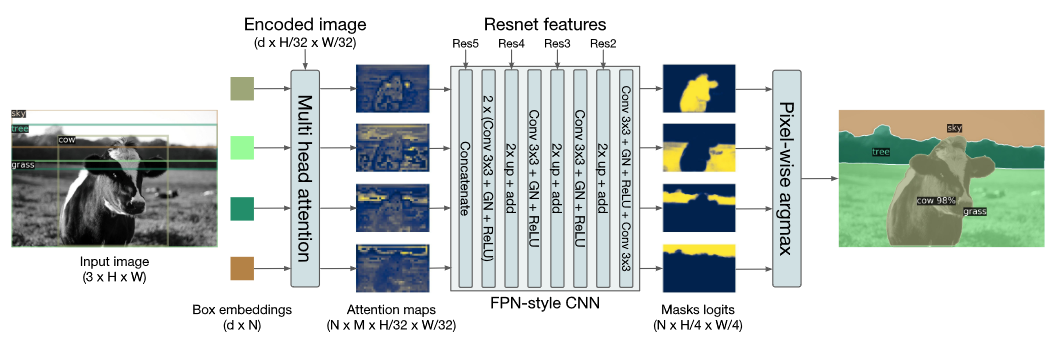
Fig. 12. DETR用于图像分割. Adapted from ^[4]

如上图所示，DETR架构也可以用于图像分割，并且也在实验中取得了比其他方法更好的结果。

Transformer和知识蒸馏

在2020年底，ViT发布两个月后，这篇论文《Training data-efficient image transformers & distillation through attention》[5]介绍了他们的新方法Data-efficient image Transformers (DeiT)，这是一个用少量数据和时间训练，就可以达到SOTA水平的方法。对于一个差不多参数量的ViT，需要一个Cloud TPU v3训练83天。而对于DeiT，只需要4个GPU训练3天，可见效率提升很大。

此外，之前的ViT需要在谷歌未公开的数据集JFT-300M用3亿张图片进行训练，而这个只需要在公开的ImageNet上训练就已经能达到SOTA的水平，所以这个模型是data-efficient的。

它主要的方法是通过知识蒸馏(knowledge distillation)的方法，并且做了不少实验，对比了不同的实验设定有怎样的效果。

它的基本结构如下图所示。

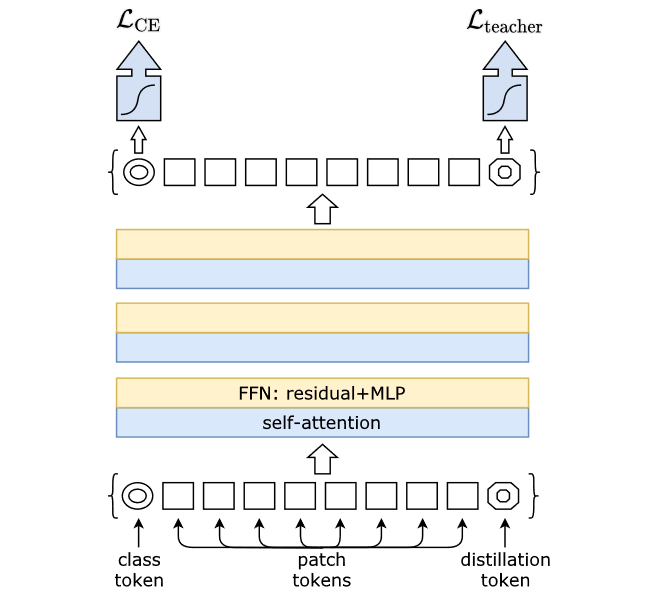
Fig. 13. DeiT架构. Adapted from ^[5]

知识蒸馏

知识蒸馏是一种知识训练方法，其中知识是由一个预训练的教师模型和一个需要训练的学生模型组成。知识蒸馏除了能有效的压缩模型，还能有效的提升学生模型的性能。

由Fig. 13可以看出，相比于之前的ViT，它多了一个知识蒸馏的部分。首先是输入部分，除了左下角的class token之外，还增加了一个右下角的distillation token。这个distillation token经过Transformer会输出一个值用于计算蒸馏损失。

蒸馏损失

关于蒸馏损失，这篇文章给出了两种方法，分别是硬蒸馏和软蒸馏。

$$\mathcal{L}_{dis}^{hard}=\frac{1}{2}\mathcal{L}_{CE}(\psi(Z_s),y)+\frac{1}{2}\mathcal{L}_{CE}(\psi(Z_s),y_t)$$

$$\mathcal{L}_{dis}^{soft}=(1-\lambda)\mathcal{L}_{CE}(\psi(Z_s),y)+\lambda\tau^2KL(\psi(Z_s/\tau),\psi(Z_t/\tau))$$

其中，$Z_t$是教师模型的logits输出，$Z_s$是学生模型的logits输出，$y_t$是老师模型的label，$y$是ground truth。$\tau$是超参数蒸馏温度，$\lambda$是蒸馏损失和交叉熵损失的比例。另外，$\mathcal{L}_{CE}$指的是交叉熵损失，$\psi()$指的是sigmoid函数。

根据作者的实验结果，硬蒸馏的训练效果更好。

教师模型的选择

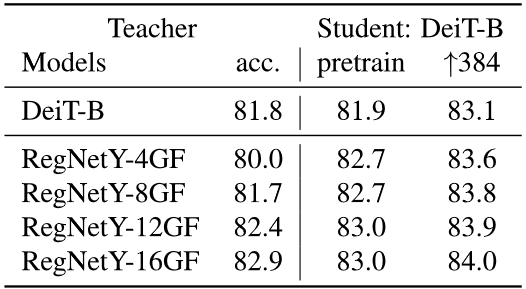
Fig. 14. 教师模型的实验结果对比. Adapted from ^[5]

作者对不同的教师模型进行了横向对比，根据上图的实验结果，可以看出使用CNN的效果要比Transformer更好。

其他超参数

作者对于训练用的很多参数都做了实验对比测试，其中包括学习率，参数初始化方法，weight decay，dropout，还有数据增强，优化器和正则化等等。对于详细的内容请参考原文，因为仅仅是实验结果而已，这里就不多做展示了。

这篇文章给Transformer使用知识蒸馏提供了很多意见和想法，如果在未来需要用一些比较高效的方法来训练Transformer，可以参考这篇文章。

参考文献

[1] A. Vaswani et al., “Attention is all you need,” in Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, Dec. 2017, pp. 6000–6010.
[2] A. Dosovitskiy et al., “An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale,” arXiv:2010.11929 [cs], Oct. 2020, [Online]. Available: http://arxiv.org/abs/2010.11929.
[3] I. Bello, B. Zoph, A. Vaswani, J. Shlens, and Q. V. Le, “Attention Augmented Convolutional Networks,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 3286–3295, [Online]. Available: https://openaccess.thecvf.com/content_ICCV_2019/html/Bello_Attention_Augmented_Convolutional_Networks_ICCV_2019_paper.html.
[4] N. Carion, F. Massa, G. Synnaeve, N. Usunier, A. Kirillov, and S. Zagoruyko, “End-to-End Object Detection with Transformers,” in Computer Vision – ECCV 2020, Cham, 2020, pp. 213–229, doi: 10.1007/978-3-030-58452-8_13.
[5] H. Touvron, M. Cord, M. Douze, F. Massa, A. Sablayrolles, and H. Jegou, “Training data-efficient image transformers & distillation through attention,” in International Conference on Machine Learning, Jul. 2021, pp. 10347–10357. Accessed: Jul. 22, 2021. [Online]. Available: http://proceedings.mlr.press/v139/touvron21a.html
[6] S. Khan, M. Naseer, M. Hayat, S. W. Zamir, F. S. Khan, and M. Shah, “Transformers in Vision: A Survey,” arXiv:2101.01169 [cs], Feb. 2021, Accessed: Apr. 23, 2021. [Online]. Available: http://arxiv.org/abs/2101.01169
[7] P. Shaw, J. Uszkoreit, and A. Vaswani, “Self-Attention with Relative Position Representations,” arXiv:1803.02155 [cs], Apr. 2018, Accessed: Jul. 25, 2021. [Online]. Available: http://arxiv.org/abs/1803.02155
[8] H. Rezatofighi, N. Tsoi, J. Gwak, A. Sadeghian, I. Reid, and S. Savarese, “Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 658–666. Accessed: Jul. 26, 2021. [Online]. Available: https://openaccess.thecvf.com/content_CVPR_2019/html/Rezatofighi_Generalized_Intersection_Over_Union_A_Metric_and_a_Loss_for_CVPR_2019_paper.html