学习AI绘画，从Diffusion和CLIP开始

AI绘画在这几个月火了起来，它能从提供的文字和图片中生成新的绘画，质量很高，而且非常有趣。这个封面就是用AI生成的^[1]。但是在使用AI绘画的过程中，搞不懂steps，sampler之类的意思。为了想要更好的使用AI绘画，也想要理解AI绘画中那些参数的含义，所以本着学习新技术的目的，写了这篇文章来学习一下AI绘画。

AI绘画

这几个月风靡的AI绘画，主要是指在统计学和计算机视觉领域，用深度学习模型从一些条件输入中生成新的图片。这些输入主要是文字或者图片。比如说封面图它就是用Anything-V3.0模型^[1]从文字直接生成的。

封面图的输入参数

masterpiece,best quality,1 girl,loli, small breasts,animal ears, cute, Age:12, Height:145, hair ribbon, cute face,shy, long hair, white hair, dress , illustration, city
Negative prompt: nsfw, lowres, bad anatomy, bad hands, text, error, missing fingers, extra digit, fewer digits, cropped, worst quality, low quality, normal quality, jpeg artifacts, signature, watermark, username, blurry,hands
Steps: 40, Sampler: Euler a, CFG scale: 13, Seed: 353263948, Size: 1216x512, Model hash: 6569e224, Clip skip: 2

对于文字生成图片而言，AI绘画系统有两个重要模块，第一个是理解文字输入，第二个是使用这个理解去生成新的图片。所幸，学术界在之前已经存在了能高质量完成这两步的技术基础。其中Denoising Diffusion Probabilistic Models (DDPM/Diffusion)^[2]提供高质量的图片生成技术，而Contrastive LanguageImage Pre-training (CLIP)^[3]提供了高水平的自然语言跨模态理解。

这篇文章我们将从DDPM和CLIP开始学习AI绘画。

DDPM

在DDPM出现之前，图片生成主要是通过变分自编码器(VAE)和生成对抗网络(GAN)来完成的。但是VAE生成的图片模糊，而GAN的训练很困难，最后生成的多样性比较有限。DDPM解决了这个难点，它能生成高质量的图片，而且也不需要对抗训练，训练起来也很简单。但是DDPM也有缺陷，它生成图片的速度比较慢，因为需要执行很多步的迭代。我们先从介绍DDPM开始。

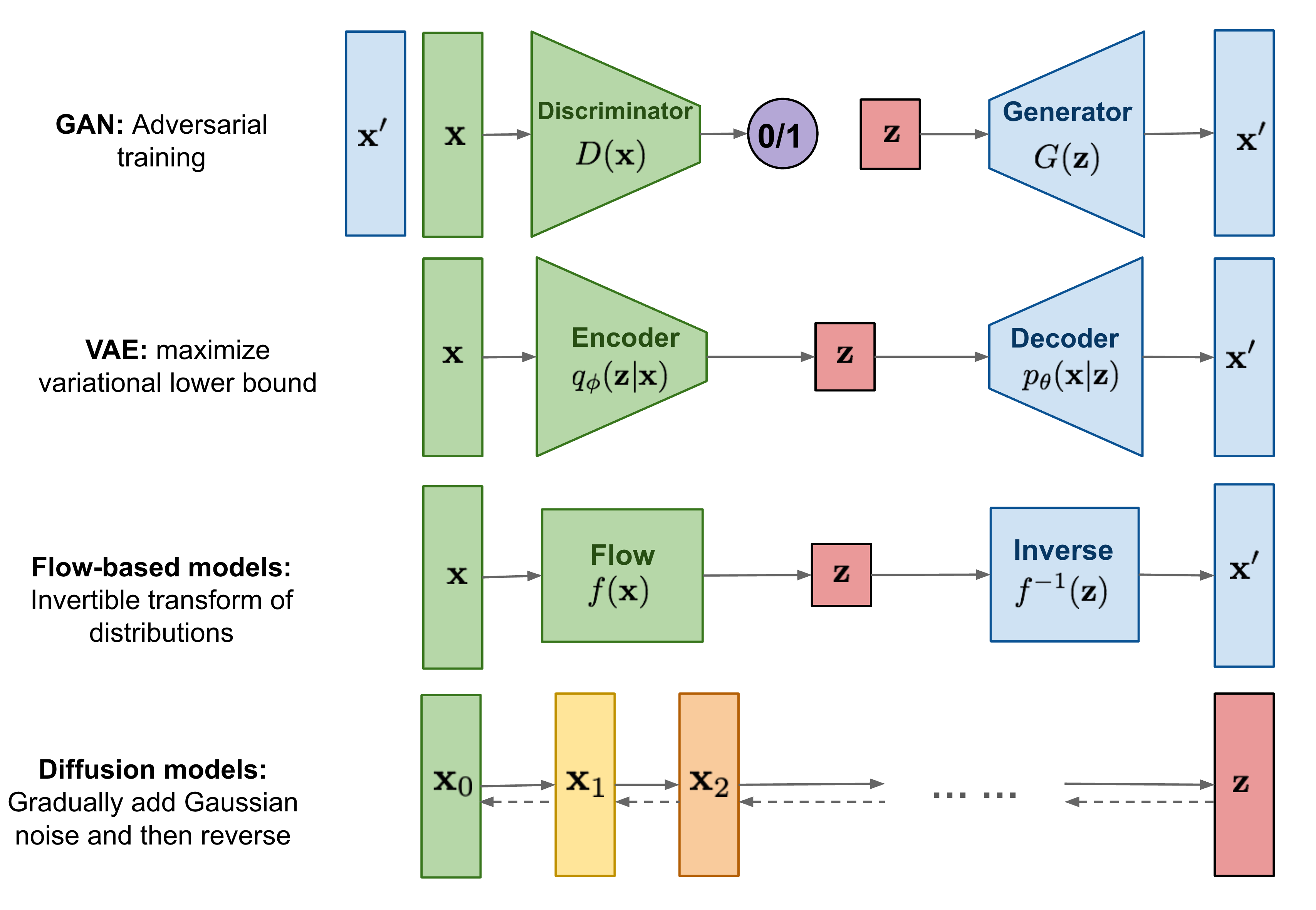
Fig. 1. 生成式模型. Adapted from ^[4]

如上图所示，DDPM是从一个生成的噪声$z$中迭代多次生成图片的，而且相比于VAE和GAN存在一个低维的隐式表示$z$，DDPM的每次迭代生成的中间图片$x_t$都保持在相同的维度上。

DDPM之所以是Diffusion(扩散)，是因为它是通过扩散过程来生成噪声，然后再训练模型去预测这个噪声来去噪，从而达到生成图片的目的。让我们先从扩散的前向过程，也就是生成噪声开始。

前向扩散

Fig. 2. 前向扩散过程. Adapted from ^[2]

首先需要定义用DDPM生成图片的过程。首先我们有一张真实图片$x_0\sim q(x)$从一个数据集中采样而来，我们希望能通过一系列手段去预测出$x_0$。

我们现在对$x_0$添加一点高斯噪声，一共添加$T$步，那么每步的结果可以表示为$x0$, $x1$, $x2$, …, $x_T$。那么每次从$x_{t-1}$添加噪声到$x_t$的过程可以表示为，

$$
\begin{equation}
x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{1 - \alpha_t}z_t
\end{equation}
$$

其中，$z_t \sim N(0, I)$是采样于标准正态分布的噪声。$\alpha_t$是一个一开始被决定好的常量，在原文中被称为步长，但是更像是一个权重，决定这一步中包含噪声的多少。这里可以看出$x_t$主要是取决于$x_{t-1}$和这个高斯分布$z_t$。所以，我们可以一步步递归计算到$x_0$，这里高斯分布被合并。

$$
\begin{equation}
x_t = \sqrt{\prod_{i=1}^t \alpha_i}x_0 + \sqrt{1 - \prod_{i=1}^t \alpha_i}z
\end{equation}
$$

为了表示简单，我们定义 $\bar{\alpha}_{t} = \prod_{i=1}^{t} \alpha_{i}$，则这个简化版的公式如下

$$
\begin{equation}
x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}z
\end{equation}
$$

我们可以认为，因为每个噪声都符合标准正态分布，所以每步加一个小噪声可以当成一口气加个大噪声，极大的简化了前向扩散过程。

代码如下。

def forward_process(x0, alpha_bar, t):
    z = torch.randn_like(x0)
    x_t = torch.sqrt(alpha_bar[t]) * x0 + torch.sqrt(1 - alpha_bar[t]) * z
    return x_t

反向扩散

既然我们已经知道了如何生成噪声，那么我们就可以通过预测这个噪声来去噪了。这个从$x_t$到$x_0$的过程就是反向扩散。

通过概率论的角度来看，这个前向扩散的过程可以记为条件概率分布的形式。其中从$x_0$加噪声到$x_t$的过程可以表示为$q(x_{t}|x_0)$。同理，我们也已知$q(x_{t-1}|x_0)$和$q(x_t|x_{t-1},x_0)$，根据贝叶斯公式，我们可以得到反向扩散的过程为，

$$
\begin{equation}
q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_{t}|x_0)}
\end{equation}
$$

为了简单表示，我们定义$\beta_t = 1 - \alpha_t$

因为$q(x_t|x_{t-1}) \sim N(\sqrt{1-\beta_{t}}x_{t-1}, \beta_{t}I)$的方差是$\beta_{t}I$，所以我们把$q(x_{t-1}|x_t,x_0)$的方差记为$\tilde{\beta}_{t}I$，而均值则是$\tilde{\mu}_t$。我们的目标是求解$\tilde{\mu}_t$和$\tilde{\beta}_t$。

化简等式(4)得，

$$
\begin{eqnarray}
q(x_{t-1}|x_t,x_0)&\propto& \exp(-\frac{1}{2}((\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}})x^2_{t-1}-(\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar{\alpha_{t-1}}}}{1-\bar{\alpha}_{t-1}}x_0)+C(x_t,x_0))) \\\
&=&\exp(-\frac{(x-\tilde{\mu}_t)^2}{2\tilde{\beta}_tI})
\end{eqnarray}
$$

省略常数项，求解以上等式，得到

$$
\begin{eqnarray}
\tilde{\mu}_t &=& \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}x_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 \\\
\tilde{\beta}_t &=& \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot \beta_t
\end{eqnarray}
$$

这时候方差已知，而均值$\tilde{\mu}_t$只和$x_t$和$x_0$有关。而对于$x_0$来说，我们可以通过等式(3)估算得到，

$$
\begin{equation}
x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1-\bar{\alpha}_t}\tilde{z}_{t})
\end{equation}
$$

其中这里的$\tilde{z}_t$是一个未知的噪声，我们需要通过模型来预测。

这里的$x_0$只是一个估算的结果，不能作为最终结果输出。

通过等式(9)，我们可以消去等式(7)中的$x_0$，得到

$$
\begin{equation}
\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha_t}}}\tilde{z}_{t})
\end{equation}
$$

然后我们就可以通过重参数化技巧来从$x_t$中采样$x_{t-1}$了。迭代这个过程，我们就可以得到$x_0$作为最终输出。

以下是这一步采样的代码实现。

def sample_x0_from_xt(xt, alpha_bar, t, pred_eps):
    return 1 / torch.sqrt(alpha_bar[t]) * (xt - torch.sqrt(1 - alpha_bar[t]) * pred_eps[t])

def sample_pred_mean_from_x0_xt(xt, x0, t, alpha, alpha_bar):
    xt_term = torch.sqrt(alpha_bar[t]) * (1 - alpha_bar[t - 1]) / (1 - alpha_bar[t]) * xt
    x0_term = torch.sqrt(alpha_bar[t - 1]) * (1 - alpha[t]) / (1 - alpha_bar[t]) * x0
    return xt_term + x0_term

def backward_process_step(xt, t, alpha_bar, alpha, beta_tilde, model):
    pred_eps = model(xt, t)
    x0 = sample_x0_from_xt(xt, alpha_bar, t, pred_eps)
    pred_mean = sample_pred_mean_from_x0_xt(xt, x0, t, alpha, alpha_bar)
    return pred_mean + torch.sqrt(beta_tilde[t]) * torch.randn_like(xt)

训练过程

在上一节我们知道，我们需要一个模型去预测噪声$\tilde{z}_t$，所以这个模型的输入是$x_t$和$t$，输出是$\tilde{z}_t$。而我们在前向扩散的过程中就已经获取了这个ground truth的噪声$z_t$，所以我们可以通过这个ground truth的噪声和预测的噪声之间的差异来训练模型。

对于DDPM来说，这个损失函数是MSE。

$$
L = ||z_t - \tilde{z}_t||_2
$$

模型架构

尽管DDPM的主要思想是在如何进行扩散上，这个模型不是重点，但是我们还是需要大致了解一下的。

首先这个模型是基于UNet^[5]的，UNet是一个经典的Encoder-Decoder图像分割模型，主要的特点是在上采样和下采样的过程中，都会通过一个跳跃连接来保留住低层次的特征信息。这个模型的架构如下图所示。

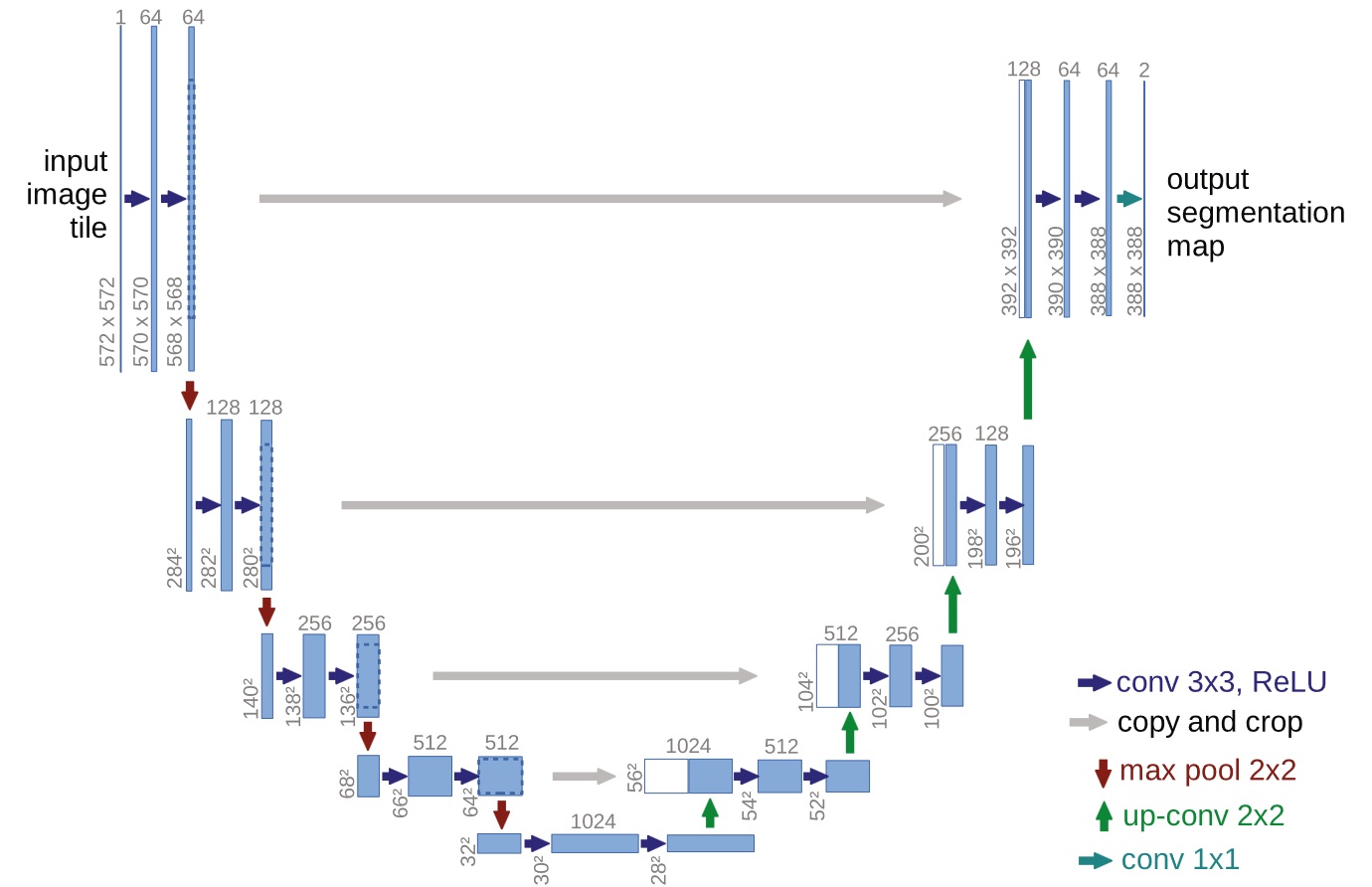
Fig. 3. U-Net. Adapted from ^[5]

相比于2015年的原版U-Net，DDPM中的每一步上采样或者下采样过程中，都有一个ResNet^[6]的残差连接结构，然后再跟上一个Multi-Head Attention层^[7]。

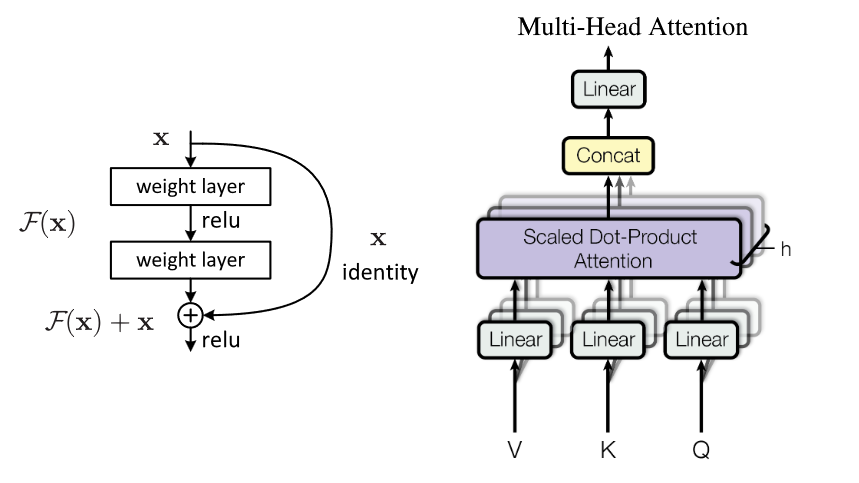
Fig. 4. 残差连接和 MultiHead Attention. Adapted from ^[6]^[7]

除此之外，对于时间信息$t$会被编码成一个embedding。如果是有条件输入的话，我们也可以把输入的条件信息(作为embedding)和time embedding相加。然后在模型的一些层中，再通过相加的方式添加到feature map中。

建立了这个模型之后，我们就可以通过前向扩散和后向扩散的过程来训练模型了。

简单测试结果

通过实现以上的代码，用了一个小参数的简单模型和简单的数据集(CIFAR10)^[8]。用了一个RTX8000训练了十几个小时，我们可以看到，模型的效果还是不错的。

Fig. 5. DDPM的简单生成结果

CLIP

介绍完了DDPM，我们再来看一下CLIP^[3]。相比于DDPM，CLIP并没有特别强的算法创新，但是它提供了一个很好的框架，用于建立自然语言和图像的关系。这个框架可以用于很多的任务，比如图像搜索，图像生成，图像分类等等。

CLIP是由OpenAI提出的多模态预训练算法，它的主要思想是通过一个超大的图像-文本数据集，来训练一个图像Encoder和一个文本Encoder。如果是相关的文本和图片，编码后的特征向量应该是相似的，如果是不相关的文本和图片，编码后的特征向量应该是不相似的。这个数据集有超过4亿个图片和文本的pair，完全是大力出奇迹。

模型架构

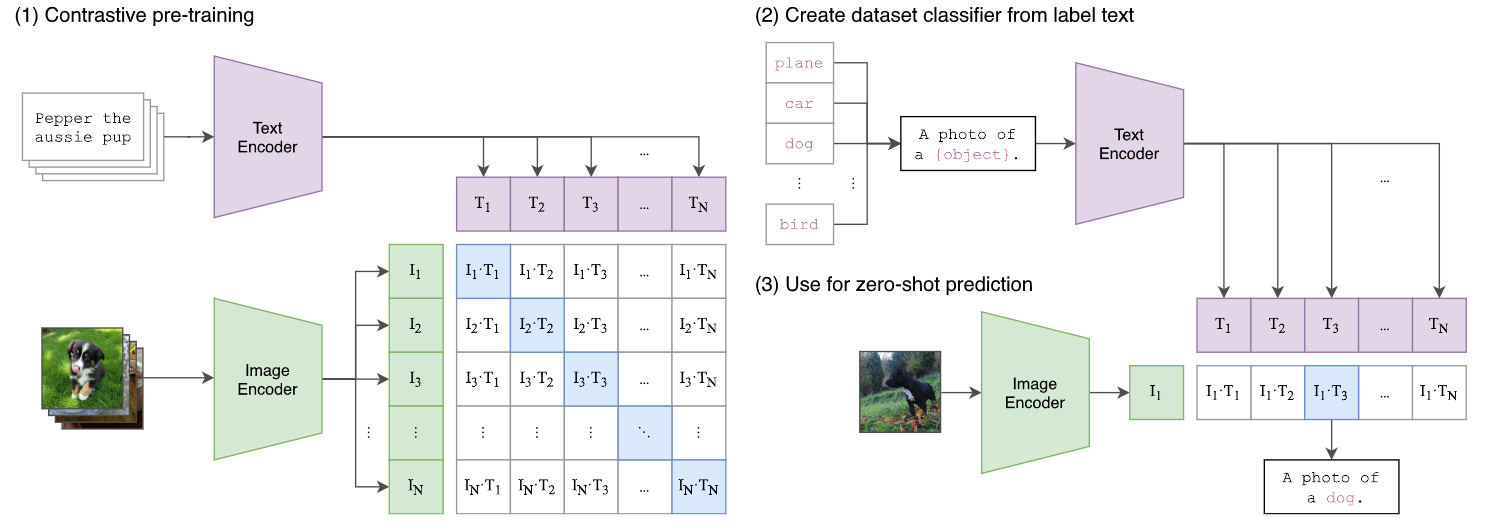
Fig. 6. CLIP的模型架构. Adapted from ^[3]

如上图所示，CLIP模型包含一个Text Encoder和一个Image Ecnoder。它们用于分别提取文本和图片的特征向量到同一个特征空间。在预训练的过程中，通过计算余弦相似度(cosine similarity)作为损失函数。原论文中也提供了伪代码来作为参考，如下所示。

# image_encoder - ResNet or Vision Transformer
# text_encoder - CBOW or Text Transformer
# I[n, h, w, c] - minibatch of aligned images
# T[n, l] - minibatch of aligned texts
# W_i[d_i, d_e] - learned proj of image to embed
# W_t[d_t, d_e] - learned proj of text to embed
# t - learned temperature parameter

# extract feature representations of each modality
I_f = image_encoder(I) #[n, d_i]
T_f = text_encoder(T) #[n, d_t]

# joint multimodal embedding [n, d_e]
I_e = l2_normalize(np.dot(I_f, W_i), axis=1) 
T_e = l2_normalize(np.dot(T_f, W_t), axis=1) 

# scaled pairwise cosine similarities [n, n] 
logits = np.dot(I_e, T_e.T) * np.exp(t) 

# symmetric loss function 
labels = np.arange(n) 
loss_i = cross_entropy_loss(logits, labels, axis=0) 
loss_t = cross_entropy_loss(logits, labels, axis=1) 
loss = (loss_i + loss_t)/2

因为整体思路较为简单，所以不再赘述。

用于下游任务

CLIP的主要用途是将预训练好的模型用于下游任务。比如说作为zero-shot图像分类任务，如图6(2,3)所示。这个任务很好的展示了这个模型的一大优势，即通过超大的文本图像数据集建立了较为充分的知识，使得模型在没有针对性的训练的情况下，也能够很好的完成下游任务。

当然，模型也可以用于图像查询。在这个任务中，只要对需要查询的文本进行编码，然后和所有图片的编码计算余弦相似度，就可以通过找最大值得到最相关的图片。

另外就是用于文字生成图片的任务了，比如说AI绘画。我们可以将文本编码为特征向量，然后将这个特征向量作为输入，作为条件信息输入到刚才提到的DDPM中。

关于如何使用CLIP，请参考OpenAI的官方Github仓库(openai/CLIP)^[9]。

总结

本文主要介绍了AI绘画的一些原理，包括了DDPM，CLIP。但是现在流行的模型Stable Diffusion (基于Latent Diffusion^[10])还没有介绍。而且AI绘画中还有很多内容，比如说sampler(DPM^[11], DDIM^[12])，这也是以后需要继续学习的方向。

参考文献

[1] Linaqruf, “Linaqruf/anything-v3.0 · Hugging Face,” huggingface.co, 2022. [Online]. Available: https://huggingface.co/Linaqruf/anything-v3.0
[2] J. Ho, A. Jain, and P. Abbeel, "Denoising Diffusion Probabilistic Models," in Advances in Neural Information Processing Systems, 2020, vol. 33, pp. 6840–6851. [Online]. Available: https://proceedings.neurips.cc/paper/2020/hash/4c5bcfec8584af0d967f1ab10179ca4b-Abstract.html
[3] A. Radford et al., “Learning Transferable Visual Models From Natural Language Supervision,” in Proceedings of the 38th International Conference on Machine Learning, Jul. 2021, pp. 8748–8763. [Online]. Available: https://proceedings.mlr.press/v139/radford21a.html
[4] L. Weng, “What are Diffusion Models?,” lilianweng.github.io, Jul. 11, 2021. [Online]. Available: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
[5] O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, Cham, 2015, pp. 234–241. doi: 10.1007/978-3-319-24574-4_28.
[6] K. He, X. Zhang, S. Ren, and J. Sun, “Identity Mappings in Deep Residual Networks,” in Computer Vision – ECCV 2016, Cham, 2016, pp. 630–645. doi: 10.1007/978-3-319-46493-0_38.
[7] A. Vaswani et al., “Attention is all you need,” in Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, Dec. 2017, pp. 6000–6010.
[8] A. Krizhevsky, “Learning Multiple Layers of Features from Tiny Images,” Master’s thesis, University of Tront, 2009.
[9] OpenAI, “CLIP,” GitHub, 2022. [Online]. Available: https://github.com/openai/CLIP
[10] R. Rombach, A. Blattmann, D. Lorenz, P. Esser, and B. Ommer, “High-Resolution Image Synthesis With Latent Diffusion Models,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 10684–10695. [Online]. Available: https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html
[11] C. Lu, Y. Zhou, F. Bao, J. Chen, C. Li, and J. Zhu, “DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps,” in Advances in Neural Information Processing Systems, Oct. 2022. [Online]. Available: https://openreview.net/forum?id=2uAaGwlP_V
[12] J. Song, C. Meng, and S. Ermon, “Denoising Diffusion Implicit Models,” in International Conference on Learning Representations, Feb. 2022. [Online]. Available: https://openreview.net/forum?id=St1giarCHLP