异星工厂中的高品质产率分析

异星工厂的品质扩展包给游戏带来了新的生产规划挑战，比起像以前只能横向扩张工厂的规模，现在可以通过使用高品质的工厂和插件，大幅增加产量。为了最大化如传奇品质的高品质物品的生产，我们需要对高品质产率的计算和规划进行一些分析。

高品质物品生产蓝图

一般来说生产高品质的物品有两种方法，生产出目标物品然后慢慢回收提升质量，或者是直接从源头生产高品质的原料，然后直接生产高品质的物品。

这里先初步的设计了两个蓝图，一个是用于电星蓝图的高品质原料生产，通过读取当前物流网络的信号，自动的将多余物品拿去回收，不断的生产高品质的原料。对于原料级别的物品（如铁板、铜板），比起直接放入回收机拿到同样的物品，将其放入到组装机里生产更高级别的物品，然后再回收回来，可以获得更高的品质。

例如下图里的：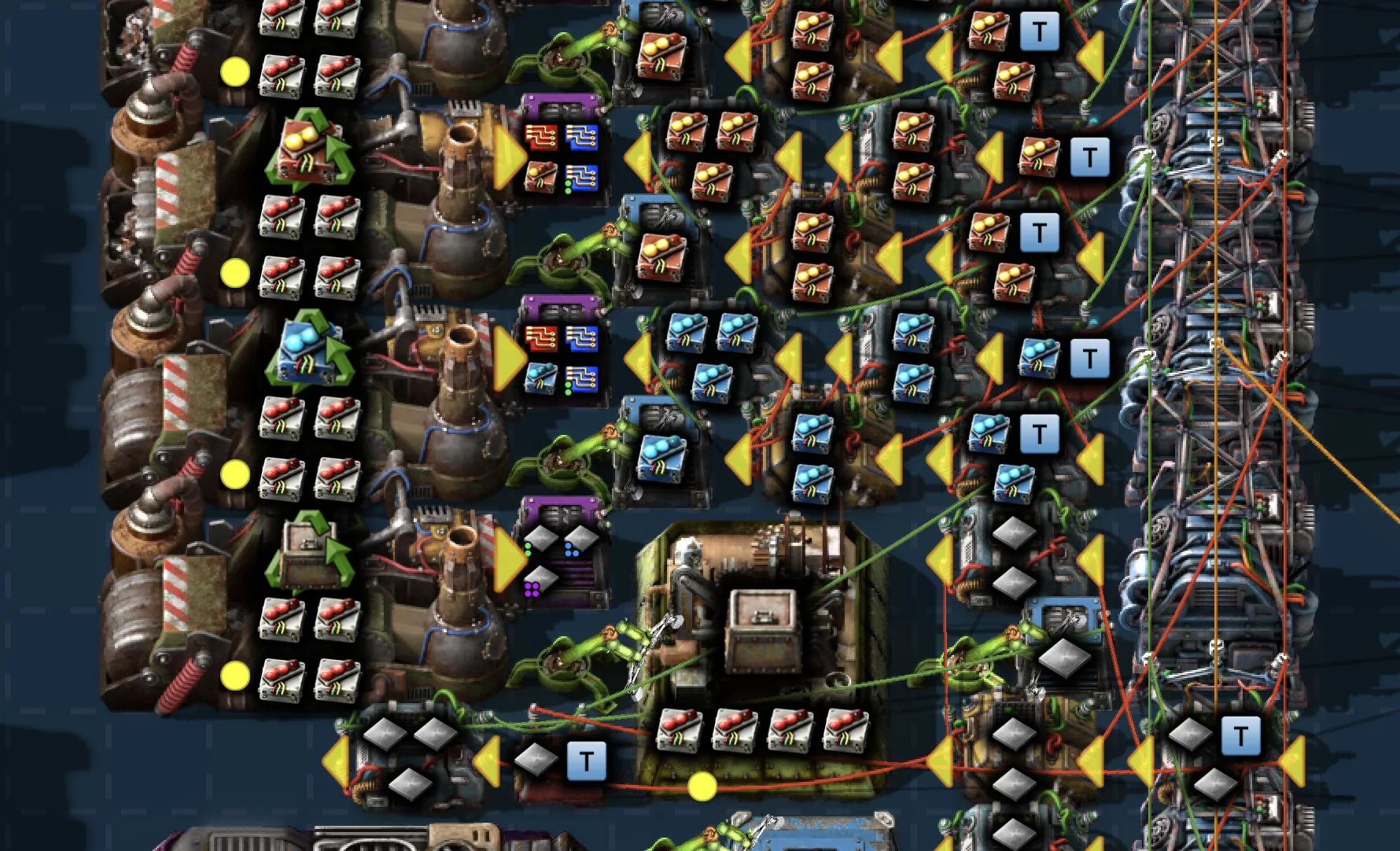

Fig. 1. 回收原料生产高品质物品的例子.

这个蓝图设计成完全全自动的模式，能自动进行负载均衡，回收多余的物品。

回收机+组装机3:

0eNrVV1tv2zYU/i98XKnWki+NDWy/Ym+pIcgykxCRKJei3BmBAGdrkHZIU2xNt16yBtmwre2wG9AWa9LAP2aVpTztL+xQkmXZlmunAzYM8ANN8nzn9p1zqC3UsjzS4ZQJ1NhCbeKanHYEdRhqoPPDfvTD9tvT/eD1IDg6Ot+5Ex68DH96GA2eDPe/D0++DU8Gwa3fwtvPhi+3w7MvwtPD4OcH0Ysfr7FrLDi7N7z9LPj9fvjo5vDrV0H/4V9v9hLE8/6jaLAbHjxNIb7cC08HsEhwh7/effvH8+DO/WDnM5Cd0f04Ot6Ldp8Hnz+NXhxFZ2fBN7vR8fGf/U8RRtR0mIsaq1vIpevMsKRPzLAJOMOJ2TMtwpEP11ibfIIaqo8LLhquS+yWRdm6YhvmBmVEKeeENL+JEWGCCkoSVfGfns48uwXwDRVnSKagXaJ0uNOlbcIVc4O4AqzsOC5NQryFAFFZWblcxagHouXq5aovrZrC1MaYnIoNmwhqKqZjtygzhMOLMCs5RIzaFPxPzlUAgzAJ7lh6i2wYXQoAIDVG1uG4HaO58mCNclfoM3HqGBwWAvwqyfC4REpJUVcYkk0KBMLpEG6kbPoArHQ80fEWYflFESjjmUTOOl1XU6drky5DLKggdpIu2s4pvu4ZFqhRbKftWUTR4kQnV+Em0ynrgiEO7yWi438ACX6am6hRktYWnqhzT7S5J2W/6cNvNgCVLAAtz9pUKHMJF4VRyNGpNp38SgFyNUMeJW8Btcb4V2P8Ija5iUZ3ch3HMKk9DLyywIHp3QJG4FGaYJ853AbqSKW2vCNNbKAP4w1P0i4NelKrGIleR8J1KRdeLJfiJxRUPr4geKlUguw0Cylau3CR1ksTcfzXinTRtXzZXlm2bPGEDToj4obDN2PjOIGaE9wjGK1zQgB2zbBcMm3QrEx8LROSCMXd4Sp+Z/cu4HBtqkYg8rQz6ZOKRtt6AUX+9w1lZfmGUrlYQ6nnevV1D2beu2ZfeQq7iPUm5aZHhQ5BJbqzpuf4CR1jdJoVhE6Y0bIy/sTZje3Qs5YzpynJWM36o5Yyh9rAh3iULzV7ly7rFHaqpvP/Vpct8YnW9RGSr5WkfOe8iyZHb3FnU8d92fVaQKzYmwLHtWz+FqG8xytG+68b5ML54b//KwdScwM8kolZ1bCKwadyE8OyjIFycllNdtV4qeEa1tIVZEQua/I8uVrDFVyPN2FDlRfUJijIdCbpT92BlpV5Ejx+Mjx4BY/44N627GvtedNXyQIqfVo8NWMOpApTDuDRooHkKJ024vzBraD/BuXk8oaGpzej73aGhyfwMTD86vWsreo/sbWZ9GnZDrMvIowso0UsqfuXvvwiia0ECy5ltsCdLgQ3VlStafVKvV6tatVaWVN9/29ridSk

回收机:

0eNrFVt1u2zYUfhdeDlRnyVYSC1ifonepIcgS0xCRJZei3BmBAGdbkXZIW3RNsP6kDTJgW3/QrgPaYksa+GFWWfLVXmGHlCz/yXFbFJh9c8TD8/GcjzwfuY2abkjajHocGdvIIYHNaJtT30MGGh720t92Ppzejv/ux0dHw+u3kv23yYsHaf/J4PavyckvyUk/vvE6ufls8HYnObubnB7GL++nb36/7F324rN7g5vP4j8Pkoc/DH5+F/ce/Pt+L0Mc9h6m/d1k/2kO8dNectoHI8Md/HHnw1/P41sH8fXvIXZu7Ufp8V66+zz+8Wn65ig9O4sf76bHx//0vkMYUdv3AmSsb6OAXvEsV9TkWS0CxTBid22XMBTBNM8h3yJDjXDJRItRvtkinNqK7bea1LO4PxmlRQ2MiMcppyRbS350TS9sNQHfUHEBZXPaIUqb+R3qEKbYmyTgkGbbD2jG8TYCREVb1S/oGHXBVPXKBT0Sic2gavj8BMtQa5OYGDkUSMhmqAAHXHHmu2aTbFodChAQN8Y2we1IvEA4NigLuDlHVttiYHCorSIoCoiIWjrNbxNm5Yfsa8jcD3k7XI4+mYPpEX7NZ1syOUYcZHAWEoyuMEIAdsNyAzKb0HyMnFYECYQoKiO/+hnka/8T+aIFuCX6WVGnqf7qY6ku5aBWcDBaYRkDlelDXV50kLESTNvQVaMmFfvuQmKzoyWJY3Q1tFxIGsY9n7WgQrFoS8wRSRroGzkQCnZk9496GiPebQu4DmU8lHE5fsaUcunTwPUK/KIG/Muo1PGcKpXxt1awN31+YCcoJ62cEGdiF/MMlZbvhC5RNClb2VRRq0m9DqTis27OZfEFkLCl9hYyKhktJR51oUdb6KkKBholFKwUFDRDd0uhXkAYX8DDWBxr9dleqpVgr07QezUEyT1Xemuz6GWn1KbMDik3gVhi+hvmRFvBURx5i641iWc13UJhADTPxCzO8oLTLviar2itqMghdnaVnN961YWELRKfHHhGeSa/1j9WiKaa4iIS92UmOwuu5mntKW+Z+mcosPrJJHzp62+pqERfUqHVyniBsAkdKFFLmFmpj5VF7M41YEbszbqGVbyGqw0MFtgVrEmzhlelVQV3XbqruJpPrMkxVVpFyBoMgqk2ALzIO9v9nJI8ZzwyDCQlc0zR4OD1cPfO8P6NuPceiWLzQNC7Yk786Mlg/x28P+N7O+L15yy6D5RiNwUHy3VcsiKEU+hT8UDGyLWaBPYEJa964oEqlx8cnoCnA/VJeH1Fq9fqdV3X9JWqpkbRf5i4IY0=

另外一种模式是通过将低级的产物不断回收，不断循环直到生产出高品质的物品，如下所示。

Fig. 1. 回收产物生产高品质物品的例子.

回收机+组装机3:

0eNrtXN1u68YRfhdeFquA+ytSQPsSuTwwBFpa28ShSIWknLoHBpoALdCLtBdBi1wmFwVaNEFboEVQoK9jJ32Lzu5KpGST4g5VnZzUB77wLrkzOzM78+3sD/UmuMw2el2meR3M3gTposirYPbqTVCl13mSmWd5stLBLEiqSq8uszS/nqySxU2a6wkP7kmQ5kv982BG70kH0VVS1ZO6TPJqXZT15FJn9R4N66Qp9eJukelyryE/bFjfrU3DjzZJltZ3AdlRZvpa58ukvNsjFfcXJNB5ndapdprZyt0836wuoZMZJceEJcG6qIC2yE3HRhT5gSTBXTBT9AN5b+R6wo+N5RcCPxIsU9DfvRcd3HnD3YxUneT1ZFGsLtM8qYuyg/t0X1piiOqyyOaX+ia5TYECmlWuv+qwDIbajSwJrtKs1uXTp1tB1kkJBXg/CUGA3aDMgrwoVzBeptOVaWMEnAU/tQ82xt3o/QX8ddlQILVUZ9Ry62y3aVlvrDpbyZw7Tj7E6cx6dZZIv5mi/EYhuSsU9+kh92oN5gBTdvCNm5F6wnVnftNw2J5AXGzq9aaeA3QVpWuc6SuDLs+ki5C6R/26d/vWIi0Xm7SelzpZzm+SfDk3rUAK8KW63GjStNg9d01XxVIbl+iQOW5kvtxkrydpXumy06KCDuARDQ/V34Bnl9cluOOyxwAiPAynQwNs4yHNwfpd1qYtMlS11tlkcaOr+pjgYY/gzNsGYe+IUdbFmeM8QvBjBnlLHkEFehyZxzi6MOocyBaREoiwG8D4dHEUhwXvHYVuM7V8jR2WaYPQV2lZ1fNnM34fCGtISAwmALAXztZ20rD4Xaw14IYVI/hJ0OAGkncnZFOFHhJ5Umh546wQOJzd5DCuK2hwGtLSyDtkJTJkY7Sppyd5Pwu9VVFDGaEvIqoBRGTMe/yR82yZlPrEsWdYUI3eAVBlAo1x0cvCOCZ940AOZSIMDZfypEyETf3iTg5lIswb1iQyE2ExLmjku5CJcHRGKU/LRDjFRql8YZkIZ+ghOSkT4dx3JpLITESv08WJMxEX3uGKzEK4RJv5tCyEK29VhrIQ7ouGQ1kIj9DR+MLmTI5F9SOpUNfuWOgdfMg0sN1APS0CBfV1WzWUNAjvXQCFnHsF9wsINZQeCDF2y5f3MJRjGbIehgobsgYtdgx/yJD1pvvQeuj/JKbJgczzXNcfF+Vrq0ypl7u06brUGvq5SrJKP5X3OY1t1hAZDt3QIfZQWmdg9KI8Pk5x60k+6eC+hbZx79zryobU9tF8CZFguoSGeETs0KqdMlZ6mW5WE6tbCU64LjJ9bJ+4z6NjtEc3IMsOLRX9QHPQ5LyTkGxnic6juyMbsvzIKYpZSSxSI5QLA7tYAM7g5Wm7qjDnb7Vebc9Slnunezung/XFJtsdIbqm5tQFWN0CmwKmIHcM09TAocFwi9fBLDTadr6hvW9Y7xtuzmMuugxIcaFopoEzhGJVbMqFnoO04Ip7hmy27O7PFraSIcO23XbsCVvJsU6p3jvlgQEF0injt+qUdh/xjA4psQ45NI9IhXRI+R4lDw2ITFjk20VJu51wRofEJjZyECFjrEO+R8jDmw4h0iHfLkIe3FE6k1cqivXKIZhUDOmV6j1MHhqQI4dEDQGF8t7lbLcH5FMfj7oYj959ED2SKuSattkzFffDMWgtP6nSX0Di0dX5FL1QVPvd//8vFBV6P3e36SDemf1ceV4LxXuXHasqvdWTdVncpktdDt9ukr34t3fw5kwy13lymTXbRV2iTEP8pSiJPCo0uNzchdwC8KbST589l81717e9mSS9rhf63wTj+1g0vAc8xV5a6IfSbv7IreF2Ae3JX47lL3ymginy2mh758ZT/CmSv0LyR179bJeLnvzjsXde/PhH4Vj5vYY38g/YCBdXEfIWvKRIwyDjVoZI/mLsvQxP/si4lQzJ3//cGImYETJkJRIxI2TISiRiRvFY/l4hFSMjViIRM0Z+riKRiBljAxeJmDEfezTuyV+Mld9veP1vwyERM0ZOtQqJaDEybhUSkWNk3CokosXIuFVIRKahd2atkJBJQ2TQKoGVnY3twMvradhGbak/2sCKp3/l024HqMGVj7lkOC+u5ntrN0qG10VkJ0W7JOn5qMtsx3TpI7Dn0U00T/u+spHk2QeMHWy2lnm+bP7R73DRUJ2wSlZ9ZvX/5KGJyg7rnvOyEw0j/LpX+ax7aRiPPoDt89O9z8GWeuEG59j5YZ+8fVs9W6ZP9nn2a69Gb/scjNLPAvNlrxump58s+231dH+HSSn6trGYIo30Y//uibLR57C9fsnRVo9fmtXRH6uYKywvy0Ry7JcCL8dE6LugUr40E01Hn+r3wls0+ki2l2U8+kjRsoTZ82MYSzN3vuKEEpjF6AV5JQgjQhEGxQieAi7TbREA1xRhfqSE0ba8e26YMNcc4pAZhsKVOWGC8F1ZKduGWT6uU2ZpHR9mJADkEq7MCaeW1jQl3LWHR9BG2DbmNYHM2rQxr4lwMsAjaONkAIWo6Ze7MsiwVda0l3RX5kSGrhwRSSSQ78pmyWArMRFERZYptGXEpAvGVoaJkYi6MnByUhgmBCJI7somqbMVbqm5oxaG2skkjc7S2cgQEhk5AlM2U6+tKEstHLXRQjnJpdXCWdIQEkUdgdUCPNtWYkstLTUQgj2YpTCNieK2kS0bx7UVZimcX5gGxPiffWM6VK5DFW0tIlwFtAqdgqYBMcmnaTYNtxXrEsayjVXs/0ZLy8oayToSZXs62KfWBO6dsDW5rUlbU9vadE8T+38rPYRA8+slLofcffi0bAHjP7/67PEP/4K6WZh1/9rJpIE5z5+vMPG87Wobz2RXmAWs7fvx668ePv/ku39//vDNFw9f/vrhd18+/v5vwVFq2VJ/95s/P/7zk+//+u3j3z99+OVnlvTCrR/NWqX54R8SZMmlzoyuf/kC+vv+H396+PaPD7/9FN7cgmWsXlKxWMSxlEwqzuj9/X8BDicdEA==

回收机+电磁工厂:

0eNrtXN1u48YVfhdetcUo0PySFNC+RC8XhkBLY5tYilRIyqm7ENAN0AK9SHvRH/QyQBCgRS7SAgmCPJB307foGY4kUvbQnEPVzm68MGAPyTNnzs93hjxnZvwqOM82el2meR3MXgXposirYPbiVVCll3mSmXt5stLBLNCZXtRlsUouc12ni8k6S6DPlgRpvtS/CWZ0Sxy9LpKqntRlklfroqwn5zrr9mHOPqVe3CwyXXYI+TFhfbM2hB9vkiytbwKy75npS50vk/Km01Vsz0ig8zqtU21Vay5u5vlmdQ6DzCh5SFgSrIsK+ha5GdiIIj+SJLgJZpJ+JGGYZQry2ufCSHmHO0NyD1HcOZK7QnEXSO5RP3cSALIAPtn8XF8l12lRmk6LtFxs0npe6mQ5v0ry5dxQgRTgqLrcaHKg2N+3pKtiqQ16HDLLg8xVrXU2WVzpyiGroF1ZHXzUgc/5Jns5SfNKlzU8uM9p2qs1ZQ7G4YFxUqb11aoJpkWxOk/zpC5cA/Be9m6rtnyN2ZYNr8o8uEjLqp7fC6PrtKwhktowshQTnSyuTCBV2rAxvKraxLyJmGKty8SKEfwCehaber1B8966LB95ejAc8GDs7UGF8yCdol0YPy8XUurnQ8kHfEiZrxMlQzqRY50o5TNzovB0YjzkROntxAjpRIV1oqLPzImhnxOVHHJi5OtEJZBOjMd+gHG3qGw6liHrYUixMONhK+GPCTPvfr82nf4/OCRHMs8hW/ikKF82ypR6uf+wuyy1hnEukqzSd+W936chO3QyHNxwZ+37Yh9hA37qut7tmsr6rjpuQx6xT3yMwhmEwt27O0HWSQkNeD6ZggD7nGUW5EW5aowIAhoaI+As+GVzY9PMDNsz+HGqyZFqqkdUcxBZKKVZv9ICHYWH1wk/jsLoR5rrJ4872TN5PPFVa7C6c47mh3c2u5eoWS8bwmG3bQ/yr0swoiXO9IVJ8u+L559T0aEZOTzWdANoLC9LgNCyZ5Jv0zTmSE53Nk9zUMUpeoR7pQj+0GhPlAqzGG0k5mEk63CXlfjUF39C4vC3yQF4KyA4DYEcWesRot8eLvbe2YoIBwDOOdp36hSAc2StR8TvAMC5RBspOg3gyhfgkuIAXialPhXcIc6FcooDt3cCIPkQuNETk2SngFsgEwIp3wFwC4o2kjgJ3IJ5gzvEgVuv08WJ4BbISrdUKHALgTZ2dBIi/Usi8UAwCYWzjKLvArjR329qehq4kR9wiuHwE/vGjuK42GmXtE4LIDn1rt8MlUPk6BUz2cOQjWUoehi2s0XVrFsWpWcZoC877mZtkMwtXk6q9Lc6cA6Oz1NVd/iffp4qJdpCcQugd6NsKx/XQgoJ4LiNB58pvSv6bq6xUXfRzAi7W/OlrmozJBDi1XJo1c767t0EjoT04bCstHktLVIjkH0VNW+eNL8s9TJtX1FmO0CtV7vS1bKz2WCvPbysNpme8KAlNUUuYHUNbAqYf23V63AFlm0mgmA2Nao6n9DeJ6z3Ce99Ikxh7Mxl1wiHFiF7ouk0tFTFplzoOUgLHu2Y+JC8bx8PWe37t9qcNxI0xYIexYVzxX+KRmf0AZ3D6FQUh05JnxSdTeb9eMhUzAuZe6XdyORYZJpvkA/IHESmQCIzfFJkNmnzIyJT+iEzfAiZCotMM8s+KTLZe4nMEIdMxZ8UmUf7LB8LnpEXPPeau+EZo+GpPsBzGJ7h1M838QO+CalvQaJN98O78I5cjEdXE5S7mhC2r98VOHmzmlgwGRQVmX6onNDHUXR2B1RVeq0n67K4Tpe6HN6wGvYu4XfKcDbjnes8Oc8OGyicokj8RtcQWTg0QXPYO7CLjge3TFRrrZe7CDnaPtC3THLgwYZ59FSjz0iwqfRdOe/by38Rm/Xby8UYuXwj+qPCve84Grv26ck/Hiu/8onqyLt+2QquvASPsIvCIc4wEXI+ahdyPfnzsUu3nvyxS8MRkr9ELu1QJH81dl3Uk384Vn4/4Puvu06RwEdGbLuu62eYGLvsypD86dhlXU/+yMCVyBkzxq5pIieeWIxdM/XkL8fK7wX82PtN2wruB/wYG7HIGTNGvmolcsaM47FLvqHnARdk5KopdgBk6CqOHYCNXe/1HYCP1cAL/HQqvNdrGQ79dIqMWyWwtsFuSZDYAZABrBR2AOx2gRA7ADaEkVMEpdgQjrED0LED+AWA/9Gv1jaeAdA5+1XqjzeQb/fn3W11IBrMu82Gl3lxMe9U1ygZzsrJXoo2+ezZgm/qMS59BLl3dtqxGX6nxv0F9PenxN9Tj6KdI2b4gkrUc+KJeu/2bLd7O6z7mLt6aOd8l3c5IvIpR9DOga+lXlhLeqwpR747NHZM72zP6F69GL1b48ikv2pqO9amd/+3gV91+qznkGuMPgccIo30vp8+ZKOPSj8fE6EPF+7Xip+PiRjaRPy5mWj0cfafpolgxv8EVDLz/QtBKGHw64zYZtQ0JTTb1u55SBiRioimyQl8RPNdExBlCKAHgS9f04SHQBw1xIaQwGeloTaPCbX84BYjiloabmiUpVHmvmjuM0MvbV9oMwK+ZLYNw1o+EAHUCNa0oRsB7zV9jTzc0pg/REytnlPTtvTAgpPQ0kA34AQvLmEv4C61oxnmRhtq2zByaNvhrkdDZIZTVn1oc6LscDImkiiwxqEdte2QN21lzGVeCIaR4WH0p7YNjKx5DQ+ipO1g2uHUtnnTmdrORlFlxVNGOWUVNf32IyvVdGC2g3Ggii1R1OEaN0TWAMZCxHz1NDiQuwvr0NgYCkRv3Gj+NrLYK9pcsd0Va644XAECDyd/7WfH/lDAsoXtf3//2Zu/fw/X5sPbfVJ4cgg2zyOZZnrYDbWbHsi+MQtYO/bt53+4/fPnb/727+DBHrLt8faP/3rz7esfvv7uzX8+vf3dZ03XM5sTmO/Pwz+SIkGWQBJo9PvqH7d/ef3DN/+8/e7L2z99+rO3f/327Rev7cXPge4abNNoJhWLRRxLyaTijG63/wPLr/8+

回收机+铸造厂:

0eNrtHF2P47bxv+ipLeRAJEWKWqD9E308LAytzd0Vzis5krzp9mAgDdC+pX0IWvTx+lCgQAs0AQqk/UF7yP2LzpD+kHcliyPHzaV7uIelrOHMcL7IGY7uTXC1WJlllRdNcPEmyGdlUQcXr94EdX5TZAv8rcjuTHARXJerYl49BOswyIu5+VVwwdZhG655WCLcp6tskTcPQbiduDA3pphnB1P5+jIMTNHkTW4cPfvwMC1Wd1emAty76ddZ3UyaKivqZVk1kyuzaAD3sqxhblkgYcAn5CcyDB5gHmOfSKAzzyszcwAxsvkEPSeiT2joBRG9oqGPiej1EfRhACpvqnIxvTK32X1eVjhrllezVd5MK5PNp7dZMZ8iFLABymqqlQl3ENvfHehdOTeo3Q6m5Y7pujFmMZndmrqD2ZgdMNuBSO0QXa0Wryd5UZuqgRfPUUX962a8A3Oyw5xVeXN7Z5p8NpmVd1d5kTVlFwXRj79bsHvEKLm5RVbji+u8qpvpM2+6z6sGHGrvTQ5iYrLZLfpTbRAN4qqbDH0YHKdcmipzbAQ/g5nlqlmuyLjXXbLXO9hlvjSTppzcVBgXOkQjh/SYeusxIeqRRZ62pod4ZIxqEjJ6YSbBuLdNSD4ob+GnOTloXSz2NS8ZU81Lko0ieWlGofyNIh1UZeKrSsWoqtR+9qaGLTf1XrFSQ8h45L1iTVwxZ54rHlQL93f8RAwiE6MPfKIHYzwaI+/BSPZ7kbR4/CH93nveL3HS9xMYwgOep4VpPiur13YxlZlvz5E3lTFA5zpb1OYpv8/nWLDdJMTQHX/4Pv5sQ96Aog6U362b2imvPhxD7rLNh3DFC3DTp79uvSSrYADvJxFwsM2TLoKirO6sFIFDhEEOL4Kf2x9WNlavL+Ff5zoT4jrVOdc5aFukVfP+VWuyI+7DpDh0RP0D7b+T827APD2MfvUSxN65g4h9oOfPckOnZ4QcVtx6t4BlBVJ0wAtz3QRdGbL3DtdKCHvisnhSLIAtyFRuK+qJ9a3MkHdkxBux5wUsppN5YvkgFkfJ/Y8ScCHIYuI+YnJK75QTcQuO5RF6XfglEX9MxK/IEktOM6zE12tjRfTaVQHuegcAJ/qtJoskPdGI/OsEeihSxBHNYCSjGUxMLFvK6EMIDDH3tTopiFZXZZU50eJiYmYgOVFn/oWCwQwhllTvkPFJASNWROEkH4TBJWQxqdOCSKyJckqJRpQS8WsafhlRJabYSYYlmW9MUBExJphlPjsxJkhOFoc4zYCk8K7I8KEoIYnHIkU8FknisUjFH0JQkMrb4hKixe1vIE80u4QoWEVUnPY2snTQyNLR5S/Zc+8WjcYY92Bs1SLNAiRTVr5Vmr7aRTulhkx79npS5782QSd1Tq4iqAP6//9VBCXIIkpbRvRh3HTI84ooJtpw2vIJn1Db5n0T0pzrXdvAsPlpOjd1gzQBkL6ujmW19pBN48ex8oA8UkzEXWKWIx9uZ7AbQV7cVGae73cM7A1pzN2mpDhvNZ5sFw17x2phJiLYg2LxEVDdA5oSOHTVyN0TCNSGgOAiwhV2vmG9b3jvG4Flycsuoakx1+PPPEV3od5vPfXqChixoB1lga11dSpVeyg1/ajUQ6GlY+63vZSaRF5KleKYUhM2rNRW+vRRqVZofMz9tJ9ShZdSVXRUqfGwUlspzUelWqHJMVfwfkpVfkpNjio1GVZqEn2fSu1iQo+5tfcT0viUI+lOEPT4lEP1YNxHyzuQ1epuYg9tFRxrl+XCHM05+lBy7wL14YKHmzW0OFDWUYx93FHvYFQ/j11K15J2/m3hV+uTTrx1uapmZmqdcdYKWLubjvXZTseaWnYVRKF6dzy1jhyeJqVp+mqxfiZ92TuCM+oqHfChlgh7fCj1vqxuHRb81JGyIe7SQe6It9Gtgq2XMaaCZjEt/GeyGFtBPp/FpMSUvlWPPNOCDz6hONeqqVXjhGhG3n37SlGdKBlwohbGPifSAyhah6E+FPtAU5lPV6AdU/V1V7YOKmnvMW9bQsei+bS8nraMiB0U2F3RbGqK7Gqx65Jbh1s2prturZ5+LjxQd3XRe4e91nK0jy2wiLVkNXuYLTqx6q2InlcSf/TJCotaKWhW1/m9mSyr8j6f91tNqxUq7elCjsQpWPWgLfZaWycz8YhPdTTxCgqToZ2Bb1LZVW2e/tbBnfRuttn7focpnvPGiUX+XzvxJyFl4LKJRckI1NoPtR7d+KU9v/BJR7d+eVJofUQ0h1zbOtDRvKZP+H0XHxusT2492k+vRl+CHNjcLwL82tIZ3dOPO/2OC91tuIwR251a3XG+SuCjs1dfCuQrrlhTNf1j/5iHUWsIKVkL1E5OTaagRn/J93L0nIxuj/TVgh7dIOlLISXrmb80PfNodPnKUwucjW7a9KVA7t7AtqsXpmdq6yz5GEb9yE6Sj2Fcju5w9aVALeaSzxg8Gd196ktBj+4/9aVAPHAr8t4gotF1TF8KxKikyHGP+mWQIsc9QT6vKvnS4p4Y32Drq4XxLba+FNTocqwvhfHdrF0UIMX8DH7ABPNVHLIQQhK7DO0QvAKHEoaQVW+HG4Ak5KGKw9gORQg5pdgMFbMAOCWENM2OYVqopYVGyBASBwTH1yFzCOEngNEORiMhh4cjUeXQc4SBsMzdGGg5FmEvYMiNHQOKUAmLB1cQxg4P/gkh3bdjhJfSjgEFcBE5RmEeTGFuNiIJ09RSQ+S4AubGQHkzlpsJFigJZZhEodyONXNj7SYLN8YJyk5A2DARFsiNlRsjryAL4cY4wbGBsDsgZCkVDihGIDhcWaAEX8TuBeoJow++QP4RLTKOf3A2jvEPTnBqszrZKBxrge7JqgsFY5l3ilT2Kd08pfgELNgn/GvpxpdgYbtPqF0dY/sVw3wfHt7/9st3f/oPPGNduPuT68kuqHl+2IresyG18Z5wO7gI+J72u3/85fGr3zy+/d3jH96+++PXwdF5cj/vu39+++6bLx4//9JOunQlayzL7f5rrjBYZOCVuL6//xlofPevvz1++9fH33/xk/df/fv9529h9FMAugfB2GVJxdM4TaXkUgnO1uv/Amh7PEw=

原理分析

如果是生产高品质的原料，比如说铜板，那么将铜板生产成铜线，就会考虑到底是使用产能插件好还是质量插件好。虽然质量插件提升了出现高品质物品的概率，但是产能插件大幅增加了产率，特别是高品质的高级产能插件，能提升相当大比例的产率，可能能生产出更多的高品质物品。

参考Figure 2，考虑以下的生产步骤：

flowchart LR
    Input[(蓝箱输入)] --> Ass[组装机] --> |低品质| Rec[回收机]
    Ass --> |高品质| Output[/红箱输出/]
    Rec --> Ass

如果以上图表没有正确渲染，请刷新页面。

令每次的产物$X$都用百分比表示，其中1代表原料投入的数量，如果是0.1，则表示剩下了10%的物品。

$$ X = (x_{普通}, x_{罕见}, x_{稀有}, x_{史诗}, x_{传奇}) $$

而每次经过组装机或者回收机，则是将原料于一个转换矩阵$T$相乘，输出则是新的产物的数量。不过在生产出传奇物品之后，会将这部分收集起来，不参与矩阵乘法。

其中$T$可以表示为

$$
\begin{align*}
T &= \begin{pmatrix}
T_{普通到普通} & T_{普通到罕见} & T_{普通到稀有} & T_{普通到史诗} & T_{普通到传奇} \\
0 & T_{罕见到罕见} & T_{罕见到稀有} & T_{罕见到史诗} & T_{罕见到传奇} \\
0 & 0 & T_{稀有到稀有} & T_{稀有到史诗} & T_{稀有到传奇} \\
0 & 0 & 0 & T_{史诗到史诗} & T_{史诗到传奇} \\
0 & 0 & 0 & 0 & T_{传奇到传奇} \\
\end{pmatrix} \\
&= (1 + P)\begin{pmatrix}
Q_{普通到普通} & Q_{普通到罕见} & Q_{普通到稀有} & Q_{普通到史诗} & Q_{普通到传奇} \\
0 & Q_{罕见到罕见} & Q_{罕见到稀有} & Q_{罕见到史诗} & Q_{罕见到传奇} \\
0 & 0 & Q_{稀有到稀有} & Q_{稀有到史诗} & Q_{稀有到传奇} \\
0 & 0 & 0 & Q_{史诗到史诗} & Q_{史诗到传奇} \\
0 & 0 & 0 & 0 & Q_{传奇到传奇} \\
\end{pmatrix}
\end{align*}
$$
其中$P$是额外产率，比如说用了产能插件之后会增加，而对于回收机来说，应该取值$P=-0.75$。而矩阵中的$Q_{*}$是指在给定总共的质量加成$Q$的情况下，计算出的
每一个品级到另一个品级的转换率。这部分的计算可以参考官方wiki^[1]。

定义每次产物的的起始状态为

$$X_{0} = (1, 0, 0, 0, 0)$$

则之后的每一次的产物状态可以表示为

$$X_{t} = X_{t-1}T_{回收机}T_{组装机}$$

但是需要注意的是，每次进入到下个循环之前，需要移除掉传奇物品，然后将其加到最终的产物中。

代码实现

当流程确定之后，就可以通过Scallop^[2]来实现这个过程。Scallop是一个用Rust实现的，基于符号推理的编程语言，可以用来解决这类问题。

type production_after_assembler(bound iter: i32, common: f32, uncommon: f32, rare: f32, epic: f32, legendary: f32)
type production_after_recycler(bound iter: i32, common: f32, uncommon: f32, rare: f32, epic: f32, legendary: f32)

type prod_rate(f32)
type qual_rate(f32)
type assembler_base_prod(f32)

type MachineType = ASSEMBLER | RECYCLER  // 0: ASSEMBLER, 1: RECYCLER
type n_slots(f32, MachineType)
type n_qual(f32, MachineType)
type n_prod(f32, MachineType)
type base_prod(f32, MachineType)
type P(f32, MachineType)
type Q(f32, MachineType)
type T_self(f32, MachineType)
type T_c2l(f32, MachineType)
type T_c2e(f32, MachineType)
type T_c2r(f32, MachineType)
type T_c2u(f32, MachineType)
type T_u2l(f32, MachineType)
type T_u2e(f32, MachineType)
type T_u2r(f32, MachineType)
type T_r2l(f32, MachineType)
type T_r2e(f32, MachineType)
type T_e2l(f32, MachineType)

rel n_slots(4, RECYCLER)
rel base_prod(-0.75, RECYCLER)  // only give 1/4 material back
rel base_prod(b_p, ASSEMBLER) = assembler_base_prod(b_p)
rel n_qual(4, RECYCLER)
rel n_prod(x, m) = n_qual(y, m) and x + y == n_s and n_slots(n_s, m)
// total production and quality rate for each machine
rel P(p_r * n_p + b_p, m) = n_prod(n_p, m) and base_prod(b_p, m) and prod_rate(p_r)
rel Q(q_r * n_q, m) = n_qual(n_q, m) and qual_rate(q_r)

// transform the quality to itself
rel T_self(1 - q, m) = Q(q, m)
// transform common to higher
rel T_c2l(q * 0.001, m) = Q(q, m)
rel T_c2e(x, m) = Q(q, m) and T_c2l(t, m) and q * 0.01 == x + t
rel T_c2r(x, m) = Q(q, m) and T_c2e(t1, m) and T_c2l(t2, m) and q * 0.1 == x + t1 + t2
rel T_c2u(x, m) = Q(q, m) and T_c2r(t1, m) and T_c2e(t2, m) and T_c2l(t3, m) and q == x + t1 + t2 + t3
// transform uncommon to higher
rel T_u2l(q * 0.01, m) = Q(q, m)
rel T_u2e(x, m) = Q(q, m) and T_u2l(t, m) and q * 0.1 == x + t
rel T_u2r(x, m) = Q(q, m) and T_u2e(t1, m) and T_u2l(t2, m) and q == x + t1 + t2
// transform rare to higher
rel T_r2l(q * 0.1, m) = Q(q, m)
rel T_r2e(x, m) = Q(q, m) and T_r2l(t, m) and q == x + t
// transform epic to higher
rel T_e2l(q, m) = Q(q, m)

rel production_after_recycler(0, 1.0, 0.0, 0.0, 0.0, 0.0) // initial state
rel production_after_assembler(
    iter, 
    (1 + p) * (c * t_self),
    (1 + p) * (c * t_c2u + u * t_self),
    (1 + p) * (c * t_c2r + u * t_u2r + r * t_self),
    (1 + p) * (c * t_c2e + u * t_u2e + r * t_r2e + e * t_self),
    (1 + p) * (c * t_c2l + u * t_u2l + r * t_r2l + e * t_e2l) + l
) = production_after_recycler(iter, c, u, r, e, l) and T_self(t_self, m) and T_c2u(t_c2u, m) 
    and T_c2r(t_c2r, m) and T_c2e(t_c2e, m) and T_c2l(t_c2l, m)
    and T_u2l(t_u2l, m) and T_u2e(t_u2e, m) and T_u2r(t_u2r, m)
    and T_r2l(t_r2l, m) and T_r2e(t_r2e, m) and T_e2l(t_e2l, m)
    and P(p, m) and m == ASSEMBLER and iter >= 0

rel production_after_recycler(
    iter + 1, 
    (1 + p) * (c * t_self),
    (1 + p) * (c * t_c2u + u * t_self),
    (1 + p) * (c * t_c2r + u * t_u2r + r * t_self),
    (1 + p) * (c * t_c2e + u * t_u2e + r * t_r2e + e * t_self),
    (1 + p) * (c * t_c2l + u * t_u2l + r * t_r2l + e * t_e2l) + l
) = production_after_assembler(iter, c, u, r, e, l) and T_self(t_self, m) and T_c2u(t_c2u, m)
    and T_c2r(t_c2r, m) and T_c2e(t_c2e, m) and T_c2l(t_c2l, m)
    and T_u2l(t_u2l, m) and T_u2e(t_u2e, m) and T_u2r(t_u2r, m)
    and T_r2l(t_r2l, m) and T_r2e(t_r2e, m) and T_e2l(t_e2l, m)
    and P(p, m) and m == RECYCLER and iter >= 0
    
rel legendary(l, n_s, n_q, p_r, q_r, b_p) = production_after_recycler(20, c, u, r, e, l) 
    and n_slots(n_s, ASSEMBLER) and n_qual(n_q, ASSEMBLER) and prod_rate(p_r) and qual_rate(q_r) and assembler_base_prod(b_p)

注意并没有直接在scallop代码中定义输入的数据，而是通过在和Python API中进行实现，方便一次编译，多次循环调用。

from scallopy import ScallopContext
from scallopy.collection import ScallopCollection
import time
import pandas as pd

# number of module slots of the "assembler" machine
possible_n_slots = [4, 5, 6, 8]
# all possible productivity module rates
possible_prod_rate = sorted(list({
    0.04, 0.05, 0.06, 0.07, 0.10, # tier 1
    0.06, 0.07, 0.09, 0.11, 0.15, # tier 2
    0.10, 0.13, 0.16, 0.19, 0.25, # tier 3
}))
# all possible quality module rates
possible_qual_rate = sorted(list({
    0.01, 0.013, 0.016, 0.019, 0.025, # tier 1
    0.02, 0.026, 0.032, 0.038, 0.05, # tier 2
    0.025, 0.032, 0.04, 0.047, 0.062, # tier 3
}))
# possible assembler base productivity 0 or 50%
possible_assembler_base_prod = [0.0, 0.5]
# number of quality modules will be 0..n_slots

# build the inputs
inputs = {
    "n_slots": [], "prod_rate": [], "qual_rate": [], "n_qual": [], "assembler_base_prod": []
}
for n_slots in possible_n_slots:
    for prod_rate in possible_prod_rate:
        for qual_rate in possible_qual_rate:
            for n_qual in range(n_slots + 1):
                for assembler_base_prod in possible_assembler_base_prod:
                    inputs["n_slots"].append([(n_slots, 0)])
                    inputs["prod_rate"].append([(prod_rate,)])
                    inputs["qual_rate"].append([(qual_rate,)])
                    inputs["n_qual"].append([(n_qual, 0)])
                    inputs["assembler_base_prod"].append([(assembler_base_prod,)])

print("Total number of inputs: ", len(inputs["n_slots"]))

ctx = ScallopContext()
ctx.import_file("model.scl")
t0 = time.time()
ctx.compile()
print("Time: ", (t1 := time.time()) - t0)

result = [
    ScallopCollection(ctx.provenance, coll) 
    for coll in ctx._internal.run_batch([["legendary"]] * len(inputs["n_slots"]), inputs, parallel=True)
]

output = [list(*each) for each in result]
print("Time: ", (t2 := time.time()) - t1)

# save to csv
output = [list(each[0]) for each in output]
df = pd.DataFrame(output)
df.to_csv("output.csv", index=False, header=["output", "n_slots", "n_qual", "prod_rate", "qual_rate", "assembler_base_prod"])

在代码中，预先定义了每一种组合（不同的产能插件和品质插件的组合，还有是否有50%自带产能），然后编译Scallop模型，把每一种可能性都放进去模拟，计算出传奇物品的总产量。

结果分析

通过以上计算的结果，画了一系列热力图，来展示不同的组合下，为了最大化传奇物品的产量，应该选择用多少产能插件和品质插件。

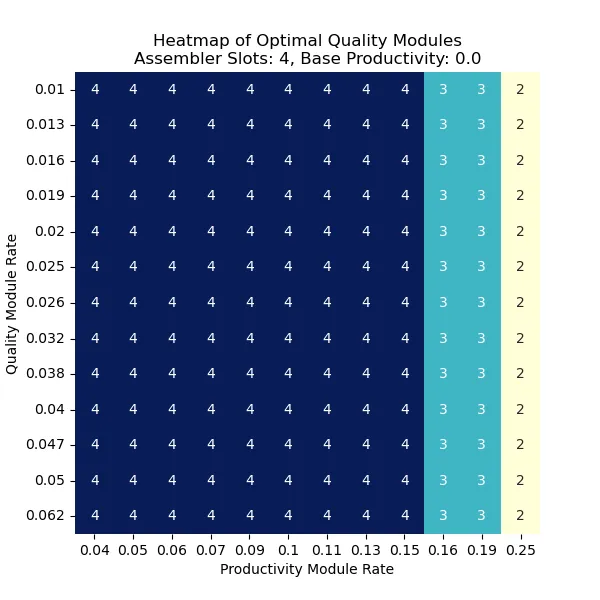
Fig. 3. 最优的品质插件数量，4插槽组装机，无基础产能加成 (组装机3型)

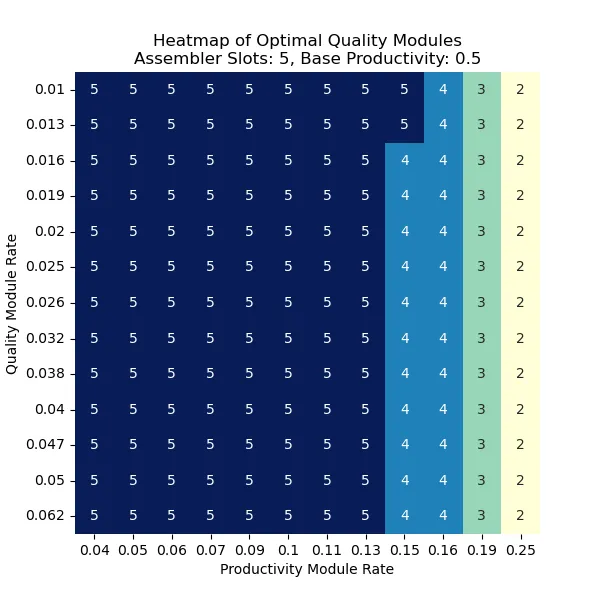
Fig. 4. 最优的品质插件数量，5插槽组装机，50%基础产能加成 (电磁工厂)

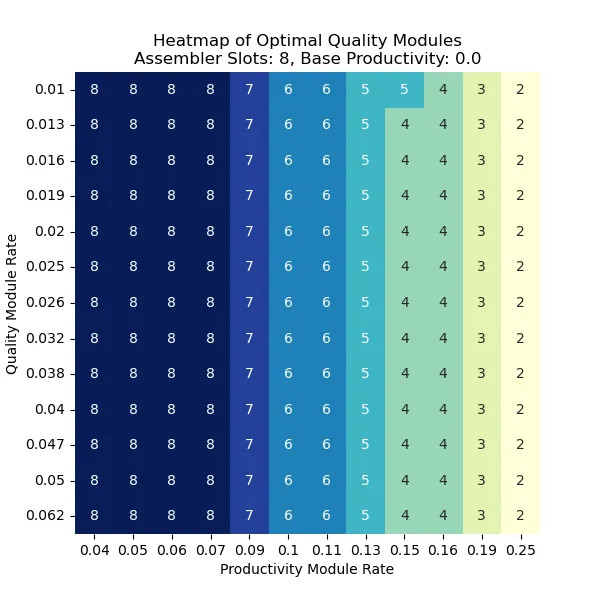
Fig. 5. 最优的品质插件数量，8插槽组装机，无基础产能加成 (低温工厂)

结论

从上图可见，最大化传奇物品的产量，并不是直接堆质量插件即可，而是需要根据产能插件和品质插件提供的加成来灵活选择，主要是考虑产能插件的数值。具体的最优化选择可以以上面几张图作为参考。

[1] "Quality", Factorio Wiki, 2024. https://wiki.factorio.com/Quality.
[2] J. Huang et al., "Scallop: From Probabilistic Deductive Databases to Scalable Differentiable Reasoning", in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2021, pp. 25134–25145. [Online]. Available: https://proceedings.neurips.cc/paper_files/paper/2021/hash/d367eef13f90793bd8121e2f675f0dc2-Abstract.html