Python编程基础06：Python的面对对象编程

人生苦短，我用Python!^[1]

这次我们来学习一下Python的面向对象编程(Object-Oriented Programming)，也被简写为OOP。OOP是一种编程思想，可以让程序有更好的扩展性，可读性和可维护性。

面对对象编程

自打程序设计这一概念出现以来，人们就一直致力于研究出可靠又易于上手易于理解的编程语言以及不同的范式，人们所最熟知的C语言便是过程式编程(Procedural Programming)^[2]的典范。这种编程范式曾经在很长的一段时间里解决了大部分人所面对的痛点——对着机器语言发愣。然而渐渐开始发现，C语言并非完美无缺，在各行各业软件愈发复杂的大前提下，C语言在很多时候会有许多不便之处，比如难以代码复用，功能拓展，项目维护，等等。为了解决这些问题，人们开始转而考虑另外一种编程范式：面向对象编程(Object Oriented Programming，简称OOP)^[2]。

在了解何为OOP之前，我们首先需要明白，C语言所谓的“过程式编程”究竟是什么，过程式编程的重点是过程，也就是“procedure”，这一词在计算机领域有“例程”的意思，所谓例程，就是一系列指令的集合所构成的一个可供执行的单元。而在C语言中，源代码便是由这些例程所组成的，一个C语言项目会使用变量和函数(也就是例程)来描述“该怎么实现程序员的意图”，而它能做到的的唯一的代码复用，也就是将重复的代码拆出来放进新的函数里面，成为一个新的“例程”以供调用。C语言之所以选择了这种编程范式是因为他是最接近机器语言的一种编程范式，计算机的机器语言本质上就是由一条条二进制的指令所组成并交给CPU执行，就像是C语言中的一个个语句一样。

正如上一节中提到的函数封装和过程分解，可以发现，实际上之前介绍的Python语法和编程思想依然基于从C语言发展而来的过程式编程。下图明确的展示了这个编程范式的结构。

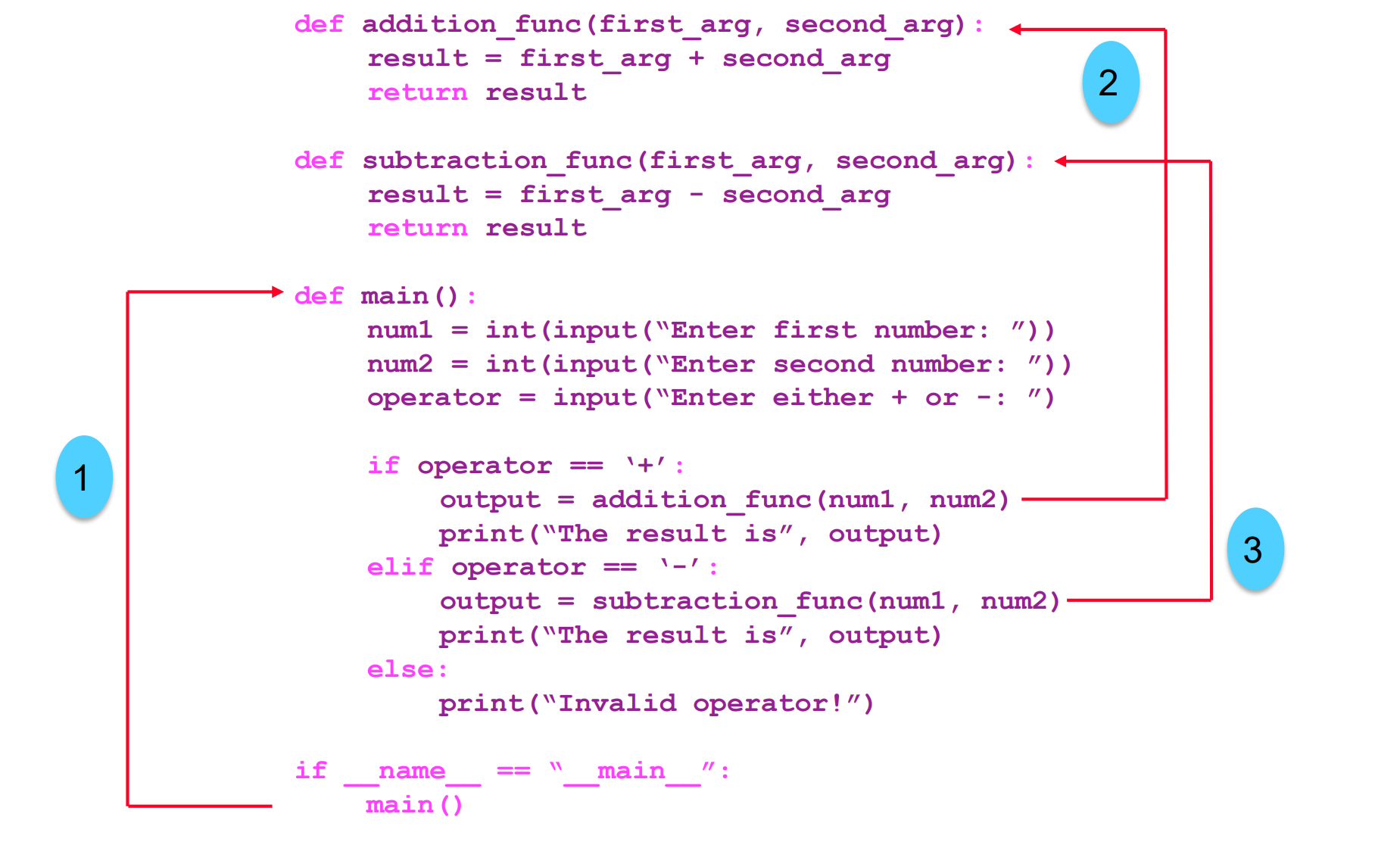
Fig. 1. 过程式编程的执行流程.

当我们提到“人”的时候，脑海中浮现出来的究竟是什么？我相信对于大部分“人”来说，这个问题的答案都是非常模糊的，我们知道人，但是仅仅是作为一个概念性的东西存在，我们需要更加详细的信息，才能对“人”这个字建立起一个更加精确地形象，比如姓名，年龄，外貌，性别等等等等，换句话说，“人”这个名词本身就像是一个模板，而这个世界上的每一个“人”，都是派生自这个模子的一个个体，这些个体补充上了前面说到的那些缺失的信息，才能让这个个体作为一个货真价实的“人”存在于这个世界上。

如果你能明白上面这段话的意思，OOP的概念对于你而言就已经熟悉了一半，上面的“人”就是一个类(class)。一个类可以拥有自己的属性和行为，但是并不能被直接拿来使用，需要以这个类为模板创造(实例化)出一个具体的东西，才能够把它拿来使用，这个东西就是对象(object)。一个类可以拥有属性(attribute)，比如性别，年龄，也可以拥有行为，也被成为方法(method)，比如吃饭，上学。OOP中的类通过对属性和行为的抽象，极强的提升了自身的表现力和抽象能力，一切东西都可以用类抽象出来。

OOP的三大要素

OOP有三大要素，分别是：封装(Encapsulation)，继承(Inheritance)，多态(Polymorphism)^[3]。它们解决了过程式编程的一些不足。

封装

让我们接着拿人作为例子，我们知道人可以吃饭，但是鲜有人知道食物在人体中消化的每一个细节，我们知道人需要呼吸，却鲜有人知道肺结构的每一部分。

封装，指的就是只对外暴露自己必要的属性和行为，而隐藏具体逻辑。一个“人”类可能可以“吃饭”，但是使用这个类不需要知道食物是如何被具体消化的，这个具体逻辑是在类的内部不可见的。简单而言：对外隐藏具体实现细节，而仅仅暴露接口。

继承

生物学中有”界门纲目科属种”的分类学^[4]，不同的物种会因为一些相似的特征而分到同一个分类中。而分类又是带层级的，真核生物里面又有动物，动物又分脊椎动物和无脊椎动物。鸟和鱼在生存环境和呼吸方式上不同，可是共同点是他们都需要摄入食物。男人和女人在身体构造上不同，可是共同点是他们都拥有名字。

这样的场景在程序开发中实在是过于常见了，比如同一个网站不同类型的账户，有的是普通账户，有的是会员账户，如果用过程式编程，那就只能硬加条件判断，并分别去写对应的逻辑，很混乱。但是OOP的继承概念就解决了这个问题。继承，指的就是一个类可以指定另外一个或者多个作为自己的父类，这样自己就可以使用父类的字段和方法，同时也可以拥有属于自己的额外属性和方法；凡是需要父类的的地方，都可以使用该父类的子类去替换，这就是里氏替换原则(Liskov Substitution Principle)^[5]。

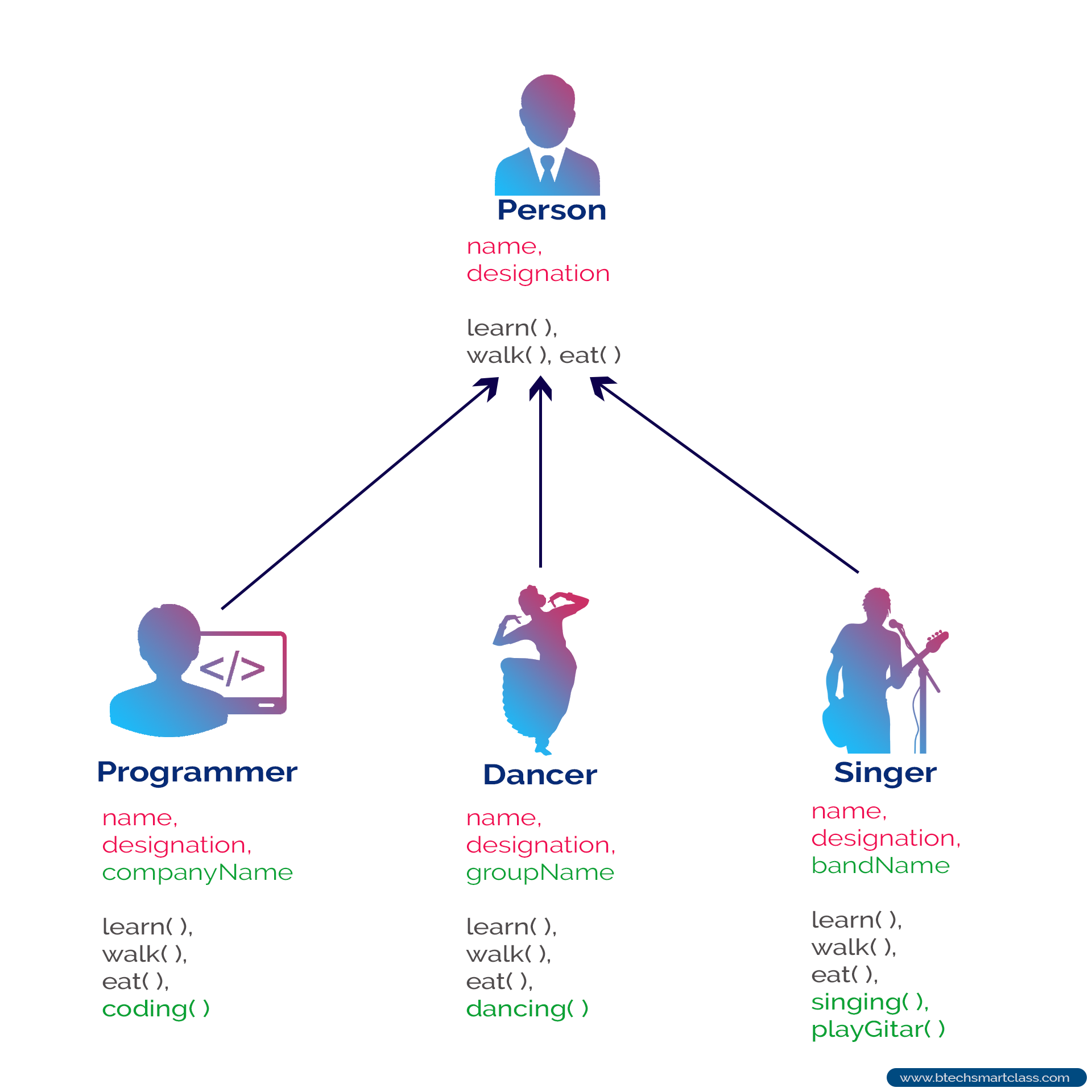
Fig. 2. OOP的继承. Adapted from ^[6]

如上图所示，父类是“Person”而子类是“Programmer”, “Dancer”和“Singer”，所以它们也构成了IS-A关系，例如“Programmer”是“Person”，所以允许里氏替换。因为“Person”都有“name”、“designation”属性和“learn”、“walk”、“eat”方法，而“Dancer”是“Person”的子类，所以“Dancer”也可以直接用“Person”的共通方法，实现了代码复用。同时，“Dancer”及其他子类也可以拥有自己的独特属性和方法，比如“groupName”属性和“dancing”方法。

多态

继承的出现引入了新的问题：对于同一个行为，不同的子类可能拥有不同的逻辑。比如鸟类和鱼类的呼吸方式，虽然鸟类和鱼类都需要呼吸，但是鸟类呼吸是通过肺，而鱼类是通过鳃。针对这一问题，OOP通过多态解决，也就是父类同一行为在不同子类上可能有着不同的实现。同样的例子，让父类“动物”提供一个方法“呼吸”，在子类“鸟”中我们重写(override)这个方法，在方法的实现中让鸟类使用肺呼吸；而在子类“鱼”中我们选择让鱼用鳃呼吸。如果需要“动物”对象，由于里氏替换原则的存在，需要“动物”的地方都可以用“动物”的子类替换，所以可以提供一个“鸟”，也可以提供一个“鱼”，由于多态的存在，虽然调用的方法都是“呼吸”，但是由于不同类型的实现不同，所以效果也会不同。

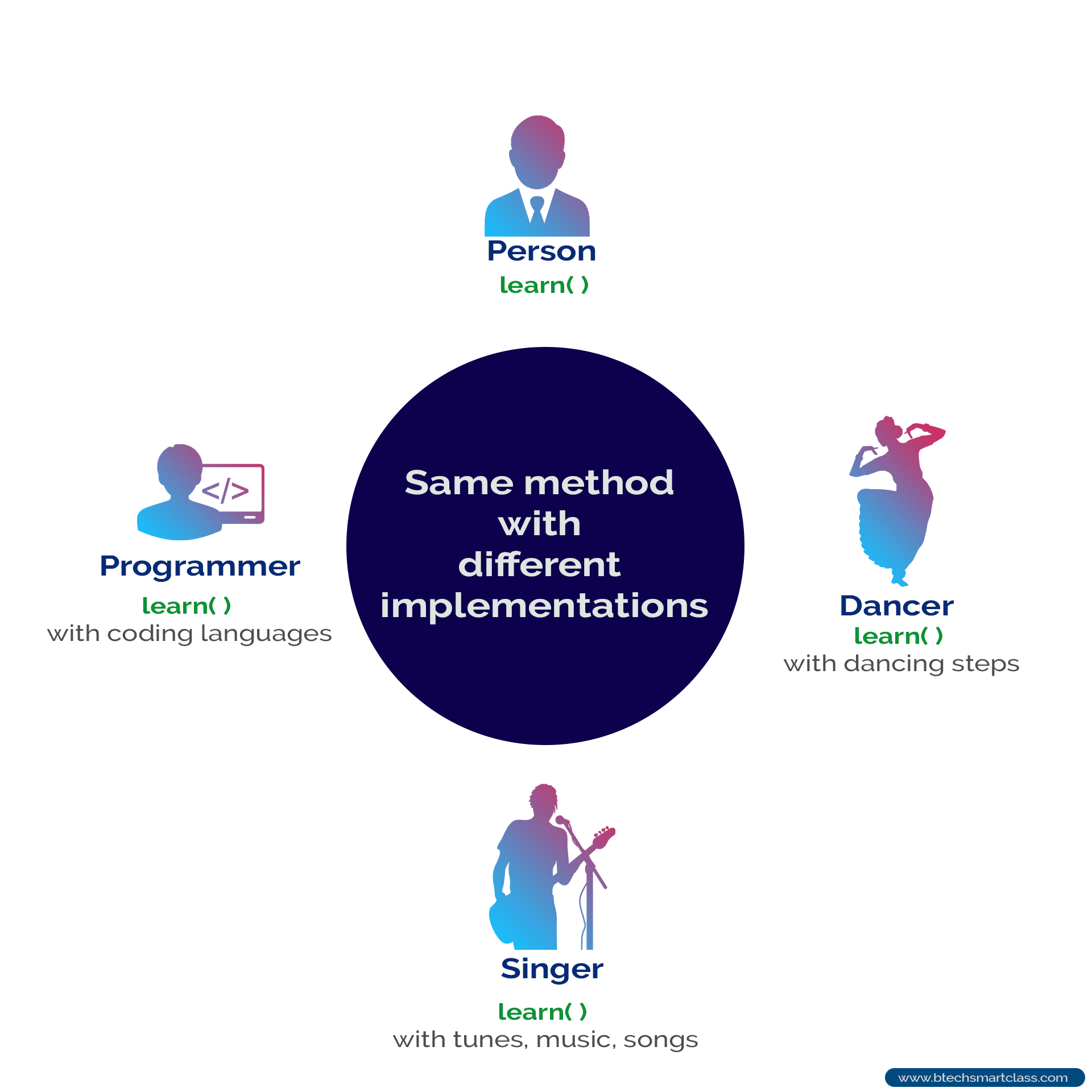
Fig. 3. OOP的多态的另一个例子. Adapted from ^[6]

Python的对象

Python支持很多类型的数据，比如说1234(int)，3.1415(float)，"Python"(str)，[1,2,3](list)，等等。这里的每一个数据都是一个对象(object)。

每一个对象都有:

一个类型(type)
一个内部数据表示(原始，复合)
一组和对象进行交互的方法

每一个对象都是一个类的实例(instance)。比如说:

1234是一个int类型的实例
"Python"是一个str类型的实例

在Python中，一切皆对象。所以在Python中，

对于某个类，可以创建新的对象
可以操作对象
可以销毁对象。比如说使用del关键字，或者直接不管它，Python会回收已销毁或者不可访问的对象，这也被称为垃圾回收(garbage collection)。

Python的类

Python中的类(class)是为了表示程序中的某一种概念而设计的，也可以被认为是定义了一种用于创建对象的模板/蓝图。在一个简单或复杂的程序中，我们需要创建很多类，每个类都有自己的职责和特性。

类的实例(instance)是从这个类中创建的对象。实例可以被赋值于一个变量，这样就可以通过这个变量来访问这个实例的内部值和相关的方法。

对于每个类，我们都会定义一些”实例变量”(instance variables) - 存储在一个实例中的内部值，和一些”方法”(methods) - 操作实例的函数。

创建一个类

创建一个类需要先指定类名，在Python中通过关键字class来定义类。比如说创建一个Point类，格式是这样的:

1 2	class Point: # define attributes here

这里在关键字class后就跟一个想要定义的类名Point，然后跟着一个冒号，接下来缩进并且定义类的内容。

注意，在Python中，类名是采用大写驼峰命名法，例如Point,CapWord,UpperCamelCase。

构造器

每一个Python中的类需要一个构造器(constructor)__init__(其中双下划线在两边)用于创建新的实例。

构造器在类中是非常重要的一部分
主要用于初始化实例的属性
通过类名进行调用

比如说在这个Point类的例子中，我们需要一个x和y分别代表一个点在平面直角坐标系的两个坐标。

class Point:
    def __init__(self, x, y): 
        self.x = x
        self.y = y

在以上例子中，__init__右边的self是代表这个实例本身，而x和y是构造器的参数。然后下面的self.x和self.y则是实例的属性，我们需要把传入的x和y值赋值给这两个属性。这样一个Point实例就会带上两个属性x和y了。

1
2
3

p = Point(1, 2)
print(p.x)  # 1
print(p.y)  # 2

这样我们就可以通过Point(...)和对应的x和y值来创建一个新的Point实例。然后通过p.x就可以访问x属性，就是在类定义中self.x所对应的值。

定义方法

类定义中的函数我们一般称为方法(method)。它就像一个函数一样，但是只能用在类中。

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        distance = (dx**2 + dy**2) ** 0.5
        return distance

上面这个例子中，我们定义了一个distance方法，它用于计算两个Point实例之间的距离。其中参数中的self代表的是这个实例本身，在使用的时候就不用再指定了。other则是另一个Point实例。

举个例子，如果要使用这个distance方法，我们可以这样写:

1
2
3

p = Point(3, 4)
origin = Point(0, 0)
print(p.distance(origin))  # 5

从上面的代码可以看到，distance中只需要传入一个参数other，而self则已经分配给了p了(写在这个方法名之前)。

但是我们还有另外一种调用方法的手段。对于同样的例子，可以这么写。

1
2
3

p = Point(3, 4)
origin = Point(0, 0)
print(Point.distance(p, origin))  # 5

在这个例子中，方法distance之前用的是Point类，而不是一个实例p，这样就可以完整的指定两个Point实例来计算了。

魔术方法

如果直接使用print来打印一个对象，会怎么样？

1 2	p = Point(3, 4) print(p) # <__main__.Point object at 0x10c8b9e58>

会发现打印的结果是包含了一个类名和所在的内存地址，对于人类来说，这个结果不是很有用。于是我们可以定义一个__str__方法，来改变打印的结果。Python会自动使用__str__方法的返回值作为打印的结果。

这样一来，Point类就是这样定义的:

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        distance = (dx**2 + dy**2) ** 0.5
        return distance

    def __str__(self):
        return "(" + str(self.x) + "," + str(self.y) + ")"

这时候再print一个Point实例，就会变成这样:

1 2	p = Point(1, 2) print(p) # (1,2)

就像这个例子中的__str__方法一样，Python中还有别的魔术方法可以用于一些特殊的目的。

比如说:

__add__(self, other) -> self + other
__sub__(self, other) -> self - other
__eq__(self, other) -> self == other
__lt__(self, other) -> self < other
__len__(self) -> len(self)
__str__(self) -> print(self)

还有很多，可以参考Python的文档^[7]。

self

类中的self参数，在方法中表示的是当前的实例本身。所以如果用一个实例来调用方法的话，就不需要再去指定self了。假设我们在point.py这个文件里定义了Point类，如下所示:

class Point:
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y
    
    def get_x(self):
        return self.x
    
    def get_y(self): 
        return self.y

    def set_x(self, x):
        self.x = x
    
    def set_y(self, y):
        self.y = y

    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        distance = (dx**2 + dy**2) ** 0.5
        return distance

这样我们就可以在别的文件里调用这个Point类，如下所示:

from point import Point
point1 = Point()
point2 = Point(1, 2)
print(point1.get_x())  # 0
print(point1.get_y())  # 0
print(point2.get_x())  # 1
print(point2.get_y())  # 2

从这里可以看出，Point类的方法中的self参数，就是当前的实例本身。

继承和多态

正如上文中提到的OOP的三大要素，Python中也可以轻松使用继承和多态。

Python中的继承通过在类名后面加上一个括号来实现。举个例子，一个平面直角坐标系上的点实际上可以当成是一个广义上二维向量的特殊形式，这里的Point类可以当成是一个Vector类的子类。

class Vector:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def get_x(self):
        return self.x
    
    def get_y(self): 
        return self.y

    def set_x(self, x):
        self.x = x
    
    def set_y(self, y):
        self.y = y

    def __str__(self):
        return "(" + str(self.x) + " " + str(self.y) + ")"

class Point(Vector):
    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        distance = (dx**2 + dy**2) ** 0.5
        return distance
    def __str__(self):
        return "<" + str(self.x) + "," + str(self.y) + ">"

这样一来，Point类继承了Vector类，并且复用了x和y属性，还有一堆getter和setter方法。而且，Point类还有一个distance方法，这是子类特有的。

而且，Vector和Point类都有__str__方法，但是它们的实现不一样，这样一来，在同样打印这些对象的时候，将会有不同的结果，这就是多态的体现。

1 2	print(Vector(1, 2)) # (1 2) print(Point(1, 2)) # <1,2>

变量的作用域

作用域(scope)的相关概念在Python中是非常重要的。这里介绍其中的主要概念。

作用域(scope)是指在一个程序中变量的访问范围。
生命周期(lifecycle)是指变量在程序执行中的存在时间。
全局变量(global variable)
- 是指在整个程序中都可以访问的变量。
- 只有在程序结束之后才会被销毁。
局部变量(local variable)
- 是指在一个函数中可以访问的变量。
- 在函数执行结束之后，这个变量就会被销毁。

def f(x):
    # ----local scope----
    x = x + 1
    print("f(x): x =", x)
    return x
    # ----local scope----

x = 3  # global scope
z = f(x)  # global scope

举个例子来说的话，上面函数f中缩进的那一部分内容都是一个局部作用域，f(x)中的x是一个局部变量。而函数之外的顶层代码，比如x = 3和z = f(x)中的x和z都是全局变量。函数内的x和函数外的x是不一样的两个变量，需要分清楚。

类中的作用域

而在class中，作用域就更加复杂了。

实例变量(instance variable)
- 和单个实例相关，并且在那个实例中是唯一的。
- 在类的内部是局部的，不能被外部直接访问(必须有实例才能访问)。
类变量(class variable)
- 在类的顶层定义的变量，和类相关，和实例无关。
- 一定程度上是全局的，只要通过类即可直接访问(也可以通过实例访问)。

class Point:
    counts = 0  # class variable

    def __init__(self, x=0, y=0):
        # x, y are local variables
        self.x = x  # self.x is an instance variable
        self.y = y  # self.y is an instance variable

访问这些变量:

print(Point.count)  # 0
print(Point.x)  # error
p = Point(1, 2)
print(p.x)  # 1
print(p.counts)  # 0

实践试试

对于刚接触OOP的同学来说，这可能是非常困难的，就算是作者也花了起码半年的时间才慢慢理解，但是我们可以通过下面的例子先来试试。这里提供了两个部分的实践，一个是继续探索并且拓展正文中提到的Point类，另一个则是写一个井字棋游戏。

探索Point类

首先来看看正文中提到的Point类。

class Point:

    def __init__(self, x, y):
        self.x = x
        self.y = y

    def get_x(self):
        return self.x

    def get_y(self):
        return self.y

    def set_x(self, x):
        self.x = x

    def set_y(self, y):
        self.y = y

    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        distance = (dx**2 + dy**2) ** 0.5
        return distance

    def __eq__(self, object):
        return self.x == object.x and self.y == object.y

    def __str__(self):
        return str(self.x) + " , " + str(self.y)

可以先试试判断一下各个变量所处的定义域。

类变量: 没有
实例变量: self.x, self.y
局部变量: dx, dy, distance

如果我们需要计算某个点到原点的距离，可以添加以下方法distance_to_origin：

1 2	def distance_to_origin(self): return self.distance(Point(0, 0))

这里我们使用了distance方法，这样就可以通过复用方法来让代码变得更加清晰简洁。

如果假设以原点为圆心，经过这个点画一个圆，计算这个圆的面积，就可以添加以下方法area_of_circle来实现。

1
2
3

import math
def area_of_circle(self):
    return math.pi * self.distance_to_origin() ** 2

如果我们创建了很多个Point，想要一直追踪创建的Point的数量，可以通过添加一个类变量count来记录。

class Point:
    count = 0

    def __init__(self, x, y):
        self.x = x
        self.y = y
        Point.count += 1

    def get_count(self):
        return Point.count

以上画的点是基于平面直角坐标系的，如果我们想要一个三维立体坐标的点，也可以定义一个类似的类Point3D来实现。

当然了，2D的Point中可以画圆来计算圆的面积，现在Point3D可以通过画球来计算球的体积。

class Point3D:
    count = 0

    def __init__(self, x, y, z):
        self.x = x
        self.y = y
        self.z = z
        Point3D.count += 1
  
    def get_count(self):
        return Point3D.count
    
    def distance(self, other):
        dx = self.x - other.x
        dy = self.y - other.y
        dz = self.z - other.z
        distance = (dx**2 + dy**2 + dz**2) ** 0.5
        return distance

    def distance_to_origin(self):
        return self.distance(Point3D(0, 0, 0))

    def volumn_of_sphere(self):
        return 4/3 * math.pi * self.distance_to_origin() ** 3
      
    def __str__(self):
        return str(self.x) + " , " + str(self.y) + " , " + str(self.z)

    def __eq__(self, object):
        return self.x == object.x and self.y == object.y and self.z == object.z

如果更进一步，我们想要一个类PointND，它能代表任意维度的点，比如三维的点，或者五维的点，其实也可以通过非常类似的方式来实现。当然这里计算的就不是球的体积而是超球体的体积了。

其中超球体的体积公式^[8]为

$$V_{n}(R)={\frac {\pi ^{n/2}}{\Gamma \left({\frac {n}{2}}+1\right)}}R^{n}$$

其中$\Gamma(n)$代表的是Gamma函数^[9]，如果$n$是正整数，则$\Gamma(n)=(n-1)!$。而Gamma函数将$n$的定义域拓展至所有非负整数的复数域上，这样就可以计算任意维度的超球体的体积。当然我们不用管那么多，Python自带的math库就有一个函数gamma可以直接计算Gamma函数。

import math

class PointND:
    count = 0
    def __init__(self, *xs):
        self.xs = xs
        self.n = len(xs)  # number of dimensions
    
    def get_count(self):
        return PointND.count
    
    def distance(self, other):
        assert self.n == other.n  # dimensions of 2 points should be the same
        distance_sq = 0  # sum up squares of differences for each dimension
        for i in range(self.n):
            dx = self.xs[i] - other.xs[i]
            distance_sq += dx ** 2
        distance = distance_sq ** 0.5
        return distance
    
    def distance_to_origin(self):
        return self.distance(PointND(*([0] * self.n)))

    def volumn_of_hypersphere(self):
        r = self.distance_to_origin()
        return math.pi ** (self.n / 2) / math.gamma((self.n / 2) + 1) * r ** self.n

    def __str__(self):
        return " , ".join(str(x) for x in self.xs)

    def __eq__(self, object):
        return self.xs == object.xs

井字棋游戏

井字棋(Tic-Tac-Toe)是一个两个玩家之间对战的游戏，游戏在一个3*3的棋盘上进行，每个棋子可以是X或O。如果一个玩家在棋盘上的某一行，某一列或者某一斜线上放置三个相同的棋子，则该玩家获胜。关于井字棋的更多信息可以参考Wiki^[10]。

在这个部分，我们将试试开发一个简单的井字棋游戏，游戏将在两个人类玩家之间进行。这个意思是在这个部分不需要写一个复杂的AI代码。

对于棋盘的表示，我们可以用一个二维列表来实现。然后对于将要定义的Game类，则需要以下这些方法:

start_game: 开始游戏
take_input: 接受玩家输入
check_for_win: 检查是否有玩家获胜
print_game: 打印棋盘状态

来试试看实现一下这个代码吧。

以下代码提供了其中一种解决思路。

class Game:

    def __init__(self):

        self.board = [['-','-','-'],['-','-','-'],['-','-','-']]
        self.player_turn = 1
        self.total_turns = 0

    def start_game(self):
        flag = True
        while flag:
            self.print_board()
            self.take_input()
            t = self.check_for_win()
            if t == True:
                self.print_board()
                flag = False

    def take_input(self):
        x = int(input("Enter value for x. Value can be between 0, 1, 2: "))
        y = int(input("Enter value for y. Value can be between 0, 1, 2: "))

        if x >= 3 or y >= 3 or x < 0 or y < 0:
            print("Invalid point!")
        elif self.board[x][y] != '-':
            print("Already occupied.")
        else:
            if self.player_turn == 1:
                self.board[x][y] = 'x'
                self.player_turn = 2
                self.total_turns += 1
            else:
                self.board[x][y] = 'o'
                self.player_turn = 1
                self.total_turns += 1

    def check_for_win(self):
        win = False
        if self.board[0][0] == 'x' and self.board[0][1] == 'x' and self.board[0][2] == 'x' or \
            self.board[1][0] == 'x' and self.board[1][1] == 'x' and self.board[1][2] == 'x' or \
            self.board[2][0] == 'x' and self.board[2][1] == 'x' and self.board[2][2] == 'x':
            print("player 1 wins!")
            win = True
        elif self.board[0][0] == 'x' and self.board[1][0] == 'x' and self.board[2][0] == 'x' or \
             self.board[0][1] == 'x' and self.board[1][1] == 'x' and self.board[2][1] == 'x' or \
             self.board[0][2] == 'x' and self.board[1][2] == 'x' and self.board[2][2] == 'x':
            print("player 1 wins!")
            win = True
        elif self.board[0][0] == 'x' and self.board[1][1] == 'x' and self.board[2][2] == 'x' or \
             self.board[0][2] == 'x' and self.board[1][1] == 'x' and self.board[2][0] == 'x':
            print("player 1 wins!")
            win = True
        elif self.board[0][0] == 'o' and self.board[0][1] == 'o' and self.board[0][2] == 'o' or \
             self.board[1][0] == 'o' and self.board[1][1] == 'o' and self.board[1][2] == 'o' or \
             self.board[2][0] == 'o' and self.board[2][1] == 'o' and self.board[2][2] == 'o':
            print("player 2 wins!")
            win = True
        elif self.board[0][0] == 'o' and self.board[1][0] == 'o' and self.board[2][0] == 'o' or \
             self.board[0][1] == 'o' and self.board[1][1] == 'o' and self.board[2][1] == 'o' or \
             self.board[0][2] == 'o' and self.board[1][2] == 'o' and self.board[2][2] == 'o':
            print("player 2 wins!")
            win = True
        elif self.board[0][0] == 'o' and self.board[1][1] == 'o' and self.board[2][2] == 'o' or \
             self.board[0][2] == 'o' and self.board[1][1] == 'o' and self.board[2][0] == 'o':
            print("player 2 wins!")
            win = True
        elif self.total_turns == 9:
            print("It is a draw.")
            win = True
        return win

    def print_board(self):
        print(self.board[0])
        print(self.board[1])
        print(self.board[2])

参考文献

[1] B. Eckel, “sebsauvage.net - Python”, Sebsauvage.net, 2021. [Online]. Available: http://sebsauvage.net/python/.
[2] "paradigms", Cs.lmu.edu, 2021. [Online]. Available: https://cs.lmu.edu/~ray/notes/paradigms/.
[3] "Object-Oriented Principles", D.umn.edu, 2021. [Online]. Available: https://www.d.umn.edu/~gshute/softeng/presentations/oo-principles.xhtml.
[4] "What is Taxonomy?", Cbd.int, 2021. [Online]. Available: https://www.cbd.int/gti/taxonomy.shtml.
[5] B. Liskov and J. Wing, "A behavioral notion of subtyping", ACM Transactions on Programming Languages and Systems, vol. 16, no. 6, pp. 1811-1841, 1994. Available: 10.1145/197320.197383.
[6] "Java Tutorials - OOP Concepts | Encapsulation | Abstraction | Inheritance | Polymorphism", Btechsmartclass.com, 2021. [Online]. Available: http://www.btechsmartclass.com/java/java-oop-concepts.html.
[7] "3. Data model — Python 3.9.7 documentation", Docs.python.org, 2021. [Online]. Available: https://docs.python.org/3/reference/datamodel.html#basic-customization.
[8] "DLMF: 5.19 Mathematical Applications", Dlmf.nist.gov, 2021. [Online]. Available: https://dlmf.nist.gov/5.19#E4.
[9] P. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function", The American Mathematical Monthly, vol. 66, no. 10, pp. 849-869, 1959. Available: 10.1080/00029890.1959.11989422.
[10] "Tic-tac-toe - Wikipedia", En.wikipedia.org, 2021. [Online]. Available: https://en.wikipedia.org/wiki/Tic-tac-toe.